题目内容
如图，在△ABC中，∠C=90°AC=8cm，AB的垂直平分线MN交AC与D，连接BD，若cos∠BDC=
,则BC的长是____________.
,则BC的长是____________.4cm
分析：根据垂直平分线的性质得出BD=AD，再利用cos∠BDC=
，即可求出CD的长，再利用勾股定理求出BC的长．
解答：解：∵∠C=90°，AC=8cm，AB的垂直平分线MN交AC于D，连接BD，
∴BD=AD，∴CD+BD=8，∵cos∠BDC=，
∴
，解得：CD=3，BD=5，∴BC=4．
点评：此题主要考查了线段垂直平分线的性质以及解直角三角形等知识，得出AD=BD，进而用CD表示出BD是解决问题的关键．
，即可求出CD的长，再利用勾股定理求出BC的长．解答：解：∵∠C=90°，AC=8cm，AB的垂直平分线MN交AC于D，连接BD，
∴BD=AD，∴CD+BD=8，∵cos∠BDC=
，∴
，解得：CD=3，BD=5，∴BC=4．点评：此题主要考查了线段垂直平分线的性质以及解直角三角形等知识，得出AD=BD，进而用CD表示出BD是解决问题的关键．
练习册系列答案
相关题目
的位置如图所示，则
的值为
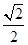
的值等于
的坡面向上走50米，则此人离地面的高度为( )
ABC中，∠B = 45°，∠C = 60°，AB = 6。求BC的长（结果保留根号）。
，AC=18，求BC、AB的长.