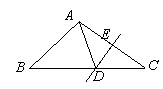题目内容
如图，△ADE为等边三角形，向两方延长DE，使得BD=DE=EC．连接AB、AC得△ABC，则∠BAC= .
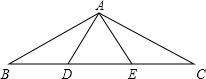
120°.
试题分析：先根据等边三角形的性质得出AD=DE=AE，∠DAE=∠ADE=∠AED=60°，再根据BD=DE=EC得出AD=BD，AE=CE，由等腰三角形的性质求出∠DAB与∠EAC的度数，进而可得出结论：
∵△ADE为等边三角形，∴AD=DE=AE，∠DAE=∠ADE=∠AED=60°.
∵BD=DE=EC，∴AD=BD，AE=CE.
∴∠DAB=∠EAC=
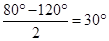．∴∠BAC=∠BAD+∠DAE+∠CAE=30°+60°+30°=120°．
练习册系列答案
相关题目
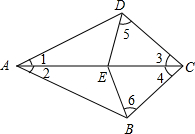
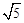， “日”字形的对角线长都为
，则八角形纸板的边长为 ．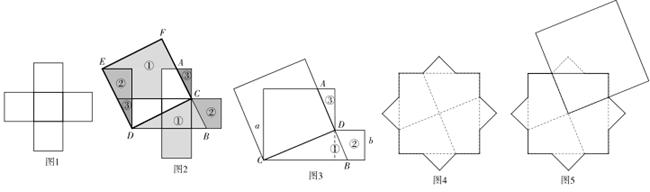
．
）
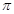