题目内容
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AC的延长线相交于点 F,且AC=8,tan∠BDC= .
.

(1)求⊙O的半径长;
(2)求线段CF长.
 .
.
(1)求⊙O的半径长;
(2)求线段CF长.
(1)5 ; (2)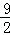
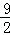
(1)作OH⊥AC于H,则AH= AC=4,
AC=4,
在Rt△AOH中,AH=4,tanA=tan∠BDC= ,
,
∴OH=3,
∴半径OA=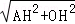 =5;
=5;
(2)∵AB⊥CD,

∴E为CD的中点,即CE=DE,
在Rt△AEC中,AC=8,tanA= ,
,
设CE=3k,则AE=4k,
根据勾股定理得:AC2=CE2+AE2,即9k2+16k2=64,
解得:k=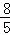 ,
,
则CE=DE=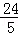 ,AE=
,AE=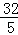 ,
,
∵BF为圆O的切线,
∴FB⊥AB,
又∵AE⊥CD,
∴CE∥FB,
∴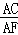 =
=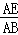 ,即
,即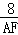 =
= ,
,
解得:AF=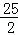 ,
,
则CF=AF﹣AC=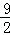 .
.
 AC=4,
AC=4,在Rt△AOH中,AH=4,tanA=tan∠BDC=
 ,
,∴OH=3,
∴半径OA=
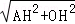 =5;
=5;(2)∵AB⊥CD,

∴E为CD的中点,即CE=DE,
在Rt△AEC中,AC=8,tanA=
 ,
,设CE=3k,则AE=4k,
根据勾股定理得:AC2=CE2+AE2,即9k2+16k2=64,
解得:k=
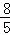 ,
,则CE=DE=
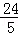 ,AE=
,AE=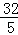 ,
,∵BF为圆O的切线,
∴FB⊥AB,
又∵AE⊥CD,
∴CE∥FB,
∴
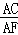 =
=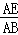 ,即
,即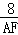 =
= ,
,解得:AF=
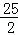 ,
,则CF=AF﹣AC=
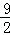 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



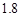 m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为 m.
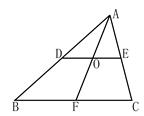
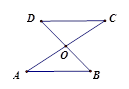
m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为 m.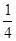 BC;③AO=FO;④
BC;③AO=FO;④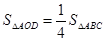 。其中正确结论的个数为( )
。其中正确结论的个数为( )