题目内容
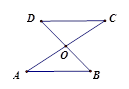
已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连结BD.
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
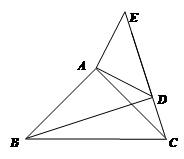
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.

(1)证明见解析;(2)BD⊥CE.
试题分析:(1)要证△BAD≌△CAE,现有AB=AC,AD=AE,需它们的夹角∠BAD=∠CAE,而由∠BAC=∠DAE=90°很易证得.
(2)BD、CE有何特殊位置关系,从图形上可看出是垂直关系,可向这方面努力.要证BD⊥CE,需证∠BDE=90°,需证∠ADB+∠ADE=90°可由直角三角形提供.
试题解析:(1)证明:∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+CAD
即∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△BAD≌△CAE(SAS).
(2)BD、CE特殊位置关系为BD⊥CE.
证明如下:由(1)知△BAD≌△CAE,
∴∠ADB=∠E.
∵∠DAE=90°,
∴∠E+∠ADE=90°.
∴∠ADB+∠ADE=90°.
即∠BDE=90°.
∴BD、CE特殊位置关系为BD⊥CE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
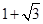 ,求△AEF的面积.
,求△AEF的面积.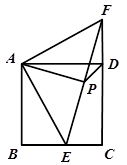


 AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.