题目内容
【题目】某商场计划采购甲、乙、丙三种型号的“格力”牌空调共25台．三种型号的空调进价和售价如下表：
种类价格 | 甲 | 乙 | 丙 |
进价（元/台） | 1600 | 1800 | 2400 |
售价（元/台） | 1800 | 2050 | 2600 |
商场计划投入总资金5万元，所购进的甲、丙型号空调数量相同，乙型号数量不超过甲型号数量的一半．若设购买甲型号空调x台，所有型号空调全部售出后获得的总利润为W元．
（1）求W与x之间的函数关系式．
（2）商场如何采购空调才能获得最大利润？
（3）由于原材料上涨，商场决定将丙型号空调的售价提高a元（a≥100），其余型号售价不变，则商场又该如何采购才能获得最大利润？
【答案】（1）
=
，（2）购进甲10台，乙5台，丙10台时利润最大
（3）即购进甲12台，乙1台，丙12台．
【解析】解：（1）由题意知：丙型号为
台，乙型号为
台，则
=
………………………………………………………………2分
（2）依题意得：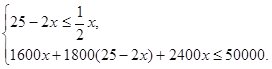
……………………………3分
解得
………………………………………………………………4分
又
为正整数
取10，11，12 ………………………………………………………………5分
随
增大而减小
当
时， 
最大．
即购进甲10台，乙5台，丙10台时利润最大．……………………………………6分
（3）依题意得： 
………………………………………………8分
当
时， 
，所以有三种方案：
即购进甲、丙两种型号各10台，乙5台
或购进甲、丙两种型号各11台，乙3台
或购进甲、丙两种型号各12台，乙1台
当
时， 
，所以当
取12时， 
最大．
即购进甲12台，乙1台，丙12台．………………………………………10分
（1）总利润=甲型号空调利润+乙型号空调利润+丙型号空调利润，根据此关系计算即可；
(2)据题意列表达式组求解；
用含x的代数式表示利润W，根据x的取值范围和一次函数的性质求解
（3）根据（1）中的等量关系可得出一个关于总利润和a的函数关系式，根据函数性质和a的取值范围，判断出不同情况下哪种利润最大．
