题目内容
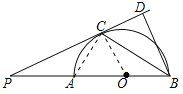
【题目】如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
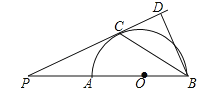
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)连接OC,由PC为圆O的切线,利用切线的性质得到OC垂直于PC,再由BD垂直于PD,得到一对直角相等,利用同位角相等两直线平行得到OC与BD平行,进而得到一对内错角相等,再由OB=OC,利用等边对等角得到一对角相等,等量代换即可得证;
(2)连接AC,由AB为圆O的直径,利用圆周角定理得到∠ACB为直角,利用两对角相等的三角形相似得到三角形ABC与三角形CBD相似,利用相似三角形对应边成比例,变形即可得证.
试题解析:(1)连接OC,∵PC与圆O相切,∴OC⊥PC,即∠OCP=90°,∵BD⊥PD,∴∠BDP=90°,∴∠OCP=∠PDB,∴OC∥BD,∴∠BCO=∠CBD,∵OB=OC,∴∠PBC=∠BCO,∴∠PBC=∠CBD;
(2)连接AC,∵AB为圆O的直径,∴∠ACB=90°,∴∠ACB=∠CDB=90°,∵∠ABC=∠CBD,∴△ABC∽△CBD,∴![]() ,则
,则![]() =ABBD.
=ABBD.

【题目】某商场计划采购甲、乙、丙三种型号的“格力”牌空调共25台.三种型号的空调进价和售价如下表:
种类价格 | 甲 | 乙 | 丙 |
进价(元/台) | 1600 | 1800 | 2400 |
售价(元/台) | 1800 | 2050 | 2600 |
商场计划投入总资金5万元,所购进的甲、丙型号空调数量相同,乙型号数量不超过甲型号数量的一半.若设购买甲型号空调x台,所有型号空调全部售出后获得的总利润为W元.
(1)求W与x之间的函数关系式.
(2)商场如何采购空调才能获得最大利润?
(3)由于原材料上涨,商场决定将丙型号空调的售价提高a元(a≥100),其余型号售价不变,则商场又该如何采购才能获得最大利润?
