题目内容
如图,延长□ABCD的边DC到E,使CE=CD,连结AE交BC于点F。
(1)试说明:△ABF≌△ECF;(4分。)
(2)连结AC、BD相交于点O,连结OF,问OF与AB有怎样的数量关系与位置关系,说明理由。(4分。)

(1)试说明:△ABF≌△ECF;(4分。)
(2)连结AC、BD相交于点O,连结OF,问OF与AB有怎样的数量关系与位置关系,说明理由。(4分。)

(1)∵AB∥CD,
∴∠E=∠BAF,∠AFB=∠EFC,
又∵CE=CD,
∴△ABF≌△ECF(AAS);
(2) OF=
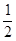 AB,OF∥AB。
AB,OF∥AB。分析:
(1)根据平行线的性质得出∠E=∠BAF,∠AFB=∠EFC,结合CE=CD=AB即可判断三角形的全等.
(2)根据题意可判断出OF是△ABC的中位线,从而可判断出数量及位置关系.
解答:
(1)∵AB∥CD,
∴∠E=∠BAF,∠AFB=∠EFC,
又∵CE=CD,
∴△ABF≌△ECF(AAS);
(2)
证明:∵OA=OC,BF=FC,
∴OF是△ABC的中位线.
故可得:OF=1/2AB,OF∥AB。
点评:此题考查了平行四边形的性质、全等三角形的判定及性质,难度一般,解答本题的关键是根据题意得出OF是△ABC的中位线。

练习册系列答案
相关题目





