题目内容
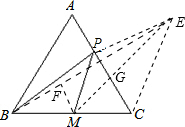
如图，正三角形ABC的边长为2，M是BC边上的中点，P是AC边上的一个动点，求PB+PM的最小值．
如图，作点B关于AC的对称点E，连接EP、EB、EM、EC，
则PB+PM=PE+PM，
因此EM的长就是PB+PM的最小值．
从点M作MF⊥BE，垂足为F，
因为BC=2，
所以BM=1，BE=2
=2
．
因为∠MBF=30°，
所以MF=
BM=
，BF=
=
，ME=
=
．
所以PB+PM的最小值是
．
则PB+PM=PE+PM，
因此EM的长就是PB+PM的最小值．
从点M作MF⊥BE，垂足为F，
因为BC=2，
所以BM=1，BE=2
| 22-12 |
| 3 |
因为∠MBF=30°，
所以MF=
| 1 |
| 2 |
| 1 |
| 2 |
| BM2-MF2 |
| ||
| 2 |
| MF2+EF2 |
| 7 |
所以PB+PM的最小值是
| 7 |
练习册系列答案
特高级教师点拨系列答案
相关题目
