题目内容
【题目】如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.
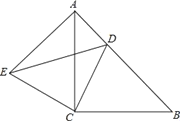
(1)求证:△BCD≌△ACE;
(2)若AD=3,BD=4,求DE的长.
【答案】(1)见解析;(2)5
【解析】
(1)根据同角的余角相等得到∠ACE=∠BCD,又夹这个角的两边分别是两等腰直角三角形的腰,利用SAS即可证明;
(2)根据全等三角形的对应边相等、对应角相等可以得到AE=BD,∠EAC=∠B=45°,所以△AED是直角三角形,利用勾股定理即可求出DE长度.
(1)证明:∵△ACB和△ECD都是等腰直角三角形,
∴AC=BC,EC=DC.
∵∠ACE=∠DCE-∠DCA,∠BCD=∠ACB-∠DCA,
∠ACB=∠ECD=90°,
∴∠ACE=∠BCD.
在△ACE和△BCD中
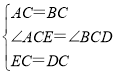 ,
,
∴△ACE≌△BCD(SAS).
(2)由(1)得,∠CAE=∠B=45°,AE=BD=4,
又∠BAC=45°
∴∠EAD=∠EAC+∠BAC=90°,
即△EAD是直角三角形,
∴![]()
∵AD=3
∴DE=![]() =5.
=5.

练习册系列答案
相关题目