题目内容
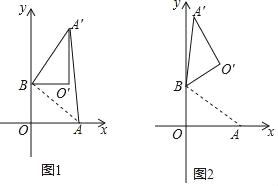
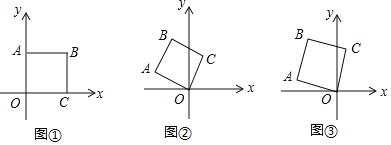
【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点.
(Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
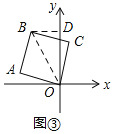
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.
【答案】(1)(﹣![]() ,1)(2)(﹣
,1)(2)(﹣![]() ,
, ![]() )
)
【解析】试题分析:(1)过点A作x轴的垂线,垂足为D,∠ADO=90°,根据旋转角得出∠AOD=30°,进而得到AD=![]() AO=1,DO=
AO=1,DO=![]() ,据此可得点A的坐标;
,据此可得点A的坐标;
(2)连接BO,过B作BD⊥y轴于D,根据旋转角为75°,可得∠BOD=30°,根据勾股定理可得BO=2![]() ,再根据Rt△BOD中,BD=
,再根据Rt△BOD中,BD=![]() ,OD=
,OD=![]() ,可得点B的坐标.
,可得点B的坐标.
解:(1)过点A作x轴的垂线,垂足为D,∠ADO=90°,
∵旋转角为60°,
∴∠AOD=90°﹣60°=30°,
∴AD=![]() AO=1,DO=
AO=1,DO=![]() ,∴A(﹣
,∴A(﹣![]() ,1);
,1);
(2)连接BO,过B作BD⊥y轴于D,
∵旋转角为75°,∠AOB=45°,
∴∠BOD=75°﹣45°=30°,
∵∠A=90°,AB=AO=2,
∴BO=2![]() ,
,
∴Rt△BOD中,BD=![]() ,OD=
,OD=![]() ,∴B(﹣
,∴B(﹣![]() ,
,![]() ).
).


练习册系列答案
相关题目
【题目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律:______________________________.
(3)根据你发现的规律填空:
①已知![]() =1.442,则
=1.442,则![]() =__________,
=__________,![]() =__________;
=__________;
②已知![]() =0.076 96,则
=0.076 96,则![]() =__________.
=__________.