Question

【题目】小丽剪了一些直角三角形纸片，她取出其中的几张进行了如下的操作：

操作一：如图，将Rt△ABC沿某条直线折叠，使斜边的两个端点A与B重合，折痕为DE.

（1）如果AC=6cm，BC=8cm，试求△ACD的周长.

（2）如果∠CAD：∠BAD=4：7，求∠B的度数.

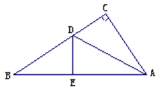
操作二：如图，小丽拿出另一张Rt△ABC纸片，将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，已知两直角边AC=6cm，BC=8cm，你能求出CD的长吗？

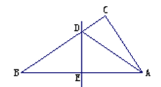
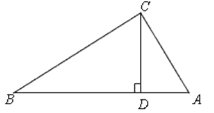
操作三：如图，小丽又拿出另一张Rt△ABC纸片，将纸片折叠，折痕CD⊥AB。你能证明：BC2+AD2=AC2+BD2吗？

Answer 1

【答案】操作一：（1）14cm；（2）∠B=35°；操作二：CD=3cm；操作三：见解析.

【解析】

操作一 利用对称找准相等的量：BD=AD，∠BAD=∠B，然后分别利用周长及三角形的内角和可求得答案；
操作二 利用折叠找着AC=AE，利用勾股定理列式求出AB，设CD=x，表示出BD，AE，在Rt△BDE中，利用勾股定理可得答案；
操作三 两次运用勾股定理可答案．

解：操作一：
（1）由对称性可得AD=BD，∵△ACD的周长=AC+CD+AD，
∴△ACD的周长=AC+CD+BD=AC+BC=8+6=14（cm）；
（2）设∠CAD=4x，∠BAD=7x由题意得方程：7x+7x+4x=90，
解之得x=5，
所以∠B=35°；
操作二：∵AC=6cm，BC=8cm，
∴AB==10cm，
根据折叠性质可得AC=AE=6cm，
∴BE=AB-AE=10-6=4，
设CD=x，则BD=8-x，DE=x，
在Rt△BDE中，由题意可得方程x2+4=（8-x）2，
解之得x=3，
∴CD=3cm；
操作三：
在Rt△BCD中，由勾股定理可得BC2=BD2+CD2
在Rt△ACD中，由勾股定理可得AD2+CD2=AC2
∴BC2+AD2=BD2+CD2+AD2=AC2+BD2