��Ŀ����
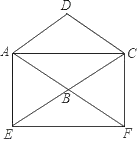
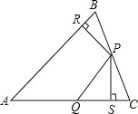
����Ŀ����֪����ABCD�͵�P������P��ͼ1�е�λ��ʱ�����н��ۣ�S��PBC=S��PAC+S��PCD
���ɣ�����P��EF��ֱBC���ֱ�AD��BC��E��F���㣮
��S��PBC+S��PAD=![]() BCPF+
BCPF+![]() ADPE=
ADPE=![]() BC��PF+PE��=
BC��PF+PE��=![]() BCEF=
BCEF=![]() S����ABCD��
S����ABCD��
��1���벹ȫ����֤�����̣�
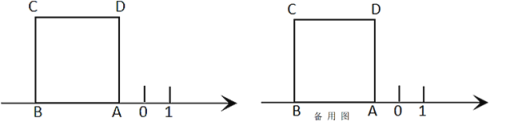
��2������ο�������Ϣ������P�ֱ���ͼ1��ͼ2�е�λ��ʱ��S��PBC��S��PAC��SPCD����������������ϵ����д�����������������IJ��룬��ѡ������һ������IJ������֤����
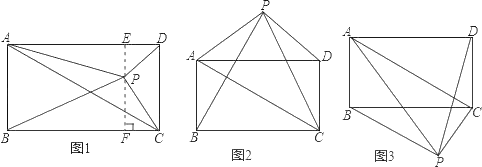
���𰸡���1��֤������������2����������ͼ2����S��PBC=S��PAC+S��PCD�� ͼ3����S��PBC=S��PAC��S��PCD��֤��������.
��������
����ͼ2���ȹ���P��EF��ֱAD���ֱ�AD��BC��E��F���㣬���������ε������ʽ��֪���������������������Եõ�S��PBC=S��PAD+![]() S����ABCD����S��PAC+S��PCD=S��PAD+
S����ABCD����S��PAC+S��PCD=S��PAD+![]() S����ABCD������S��PBC=S��PAC+S��PCD��
S����ABCD������S��PBC=S��PAC+S��PCD��
��1��֤������S��PAC+S��PCD+S��PAD=![]() S����ABCD,
S����ABCD,
��S��PBC+S��PAD=S��PAC+S��PCD+S��PAD��
��S��PBC=S��PAC+S��PCD��
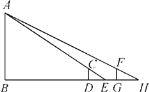
��2����������ͼ2����S��PBC=S��PAC+S��PCD�� ͼ3����S��PBC=S��PAC��S��PCD��
֤������ͼ������P��EF��ֱAD���ֱ�AD��BC��E��F���㣮
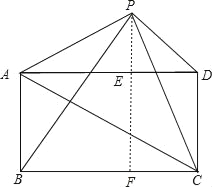
��S��PBC=![]() BCPF=
BCPF=![]() BCPE+
BCPE+![]() BCEF
BCEF
=![]() ADPE+
ADPE+![]() BCEF=S��PAD+
BCEF=S��PAD+![]() S����ABCD
S����ABCD
S��PAC+S��PCD=S��PAD+S��ADC=S��PAD+![]() S����ABCD
S����ABCD
��S��PBC=S��PAC+S��PCD��

 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ����ʦ����ѧ������ϵ�д�
ͬ����ϰ����ʦ����ѧ������ϵ�д�����Ŀ����������ͨ�����ҽ���������ũ��Ʒ��������������ɱ���͡�������һũ����Ҫ��A��B����ũ��Ʒ������������ij�ӹ�����ÿ������A��B��Ʒ�ļ������䣬ԭ��ÿ��һ�ε��˷���1200Ԫ������ÿ��һ�ε��˷ѱ�ԭ��������300Ԫ��A��B���ֲ�Ʒԭ�����˷Ѻ����ڵ��˷ѣ���λ��Ԫ�M�������±���ʾ��
Ʒ�� | A | B |
ԭ�����˷� | 45 | 25 |
���ڵ��˷� | 30 | 20 |
��1����ÿ�������ũ��Ʒ��A��B��Ʒ���ж��ټ���
��2�����ڸ�ũ����ʵ���ţ���Ʒ�����ã��ӹ���������߸�ũ���Ĺ�������ÿ�����͵��ܼ�������8�������ܼ�����B��Ʒ�ļ������ó���A��Ʒ������2�����ʲ�Ʒ�������Ӻ�ÿ���˷�������Ҫ����Ԫ��