题目内容
【题目】如图,正方形ABCD的边AB在数轴上,数轴上点A表示的数为-1,正方形ABCD的面积为16.
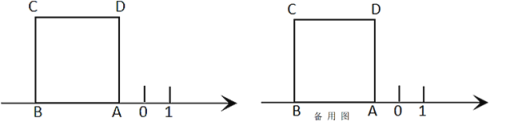
(1)数轴上点B表示的数为___;
(2)将正方形ABCD沿数轴水平移动,移动后的正方形记为A′B′C′D′,移动后的正方形A′B′C′D′与原正方形ABCD重叠部分的面积为S.
①当S=4时,画出图形,并求出数轴上点A′表示的数;
②设正方形ABCD的移动速度为每秒2个单位长度,点E为线段AA′的中点,点F在线段BB′上,且BF=![]() BB′.经过t秒后,点E,F所表示的数互为相反数,直接写出t的值.
BB′.经过t秒后,点E,F所表示的数互为相反数,直接写出t的值.
【答案】(1)-5;(2)①点A'表示的数为-4或2;②t=4.
【解析】
(1)利用正方形ABCD的面积为16,可得AB长,再根据AO=1,进而可得点B表示的数;
(2)①先根据正方形的面积为16,可得边长为4,当S=4时,分两种情况:正方形ABCD向左平移,正方形ABCD向右平移,分别求出数轴上点A′表示的数;
②当正方形ABCD沿数轴负方向运动时,点E,F表示的数均为负数,不可能互为相反数,不符合题意;当点E,F所表示的数互为相反数时,正方形ABCD沿数轴正方向运动,再根据点E,F所表示的数互为相反数,列出方程即可求得t的值.
解:(1)∵正方形ABCD的面积为16,
∴AB=4,
∵点A表示的数为-1,
∴AO=1,
∴BO=5,
∴数轴上点B表示的数为-5,
故答案为:-5.
(2)①∵正方形的面积为16,
∴边长为4,
当S=4时,分两种情况:
若正方形ABCD向左平移,如图1,
A'B=4÷4=1,
∴AA'=4-1=3,
∴点A'表示的数为-1-3=-4;
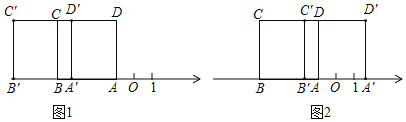
若正方形ABCD向右平移,如图2,
AB'=4÷4=1,
∴AA'=4-1=3,
∴点A'表示的数为-1+3=2;
综上所述,点A'表示的数为-4或2;
②t的值为4.
理由如下:
当正方形ABCD沿数轴负方向运动时,点E,F表示的数均为负数,不可能互为相反数,不符合题意;
当点E,F所表示的数互为相反数时,正方形ABCD沿数轴正方向运动,如图3,
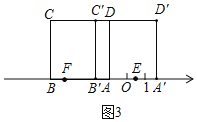
∵AE=![]() AA'=
AA'=![]() ×2t=t,点A表示-1,
×2t=t,点A表示-1,
∴点E表示的数为-1+t,
∵BF=![]() BB′=
BB′=![]() ×2t=
×2t=![]() t,点B表示-5,
t,点B表示-5,
∴点F表示的数为-5+![]() t,
t,
∵点E,F所表示的数互为相反数,
∴-1+t+(-5+![]() t)=0,
t)=0,
解得t=4.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案