题目内容
【题目】如图,已知直线AB∥CD,直线L和直线AB,CD分别交于点E,F,直线L上有一动点P.

(1)如图1,点P在E,F之间运动时,∠PMB,∠MPN,∠PND之间有什么关系,并说明理由;
(2)若点P在E,F两点外侧运动时,如图2和图3(P点与E,F不重合),试直接写出∠PMB,∠MPN,∠PND之间有什么关系,不必写理由.
【答案】(1)∠PMB+∠MPN+∠PND=360°,理由见解析;(2)∠MPN=∠PMB﹣∠PND或∠MPN=∠PND﹣∠PMB
【解析】
(1)作PG∥AB,如图1,先判断CD∥PG,再利用平行线的性质得到∠PMB+∠MPG=180°,∠PND+∠NPG=180°,两式相加得到∠PMB+∠MPN+∠PND=360°;
(2)作PG∥AB,同样得到∠AMB+∠MPG=180°,∠PND+∠NPG=180°,两式相减,在图2中得到∠MPN=∠PMB﹣∠PND;在图3中得到∠MPN=∠PND﹣∠PMB.
解:(1)∠PMB+∠MPN+∠PND=360°.
理由如下:
作PG∥AB,如图1,
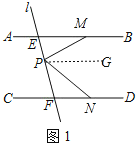
∵AB∥CD,
∴CD∥PG,
∴∠PMB+∠MPG=180°,∠PND+∠NPG=180°,
∴∠PMB+∠MPG+∠PND+∠NPG=360°,
即∠PMB+∠MPN+∠PND=360°;
(2)作PG∥AB,
∵AB∥CD,
∴CD∥PG,
∴∠PMB+∠MPG=180°,∠PND+∠NPG=180°,
即∠MPG=180°﹣∠PMB,∠NPG=180°﹣∠PND,
在图2中,
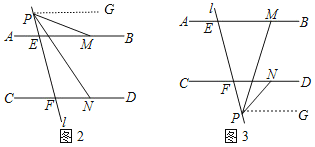
有∠NPG﹣∠MPG=∠PMB﹣∠PND,
即∠MPN=∠PMB﹣∠PND;
在图3中,∠MPG﹣∠NPG=∠PND﹣∠PMB,
即∠MPN=∠PND﹣∠PMB,
综上所述,∠MPN=∠PMB﹣∠PND或∠MPN=∠PND﹣∠PMB;