题目内容
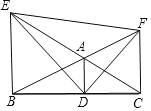
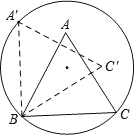
【题目】如图,正△ABC 的边长为 2,顶点 B、C 在半径为![]() 的圆上,顶点 A在圆内,将正△ABC 绕点 B 逆时针旋转,当点 A 第一次落在圆上时,则点 C 运动的路线长为 (结果保留π);若 A 点落在圆上记做第 1 次旋转,将△ABC 绕点 A 逆时针旋转,当点 C 第一次落在圆上记做第 2 次旋转,再绕 C 将△ABC 逆时针旋转,当点 B 第一次落在圆上,记做第 3 次旋转……,若此旋转下去,当△ABC 完成第 2017 次旋转时,BC 边共回到原来位置 次.
的圆上,顶点 A在圆内,将正△ABC 绕点 B 逆时针旋转,当点 A 第一次落在圆上时,则点 C 运动的路线长为 (结果保留π);若 A 点落在圆上记做第 1 次旋转,将△ABC 绕点 A 逆时针旋转,当点 C 第一次落在圆上记做第 2 次旋转,再绕 C 将△ABC 逆时针旋转,当点 B 第一次落在圆上,记做第 3 次旋转……,若此旋转下去,当△ABC 完成第 2017 次旋转时,BC 边共回到原来位置 次.
【答案】![]() ,168.
,168.
【解析】
首先连接OA′、OB、OC,再求出∠C′BC的大小,进而利用弧长公式问题即可解决.因为△ABC是三边在正方形CBA′C″上,BC边每12次回到原来位置,2017÷12=168.08,推出当△ABC完成第2017次旋转时,BC边共回到原来位置168次.
如图,连接OA′、OB、OC.
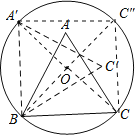
∵OB=OC=![]() ,BC=2,
,BC=2,
∴△OBC是等腰直角三角形,
∴∠OBC=45°;
同理可证:∠OBA′=45°,
∴∠A′BC=90°;
∵∠ABC=60°,
∴∠A′BA=90°-60°=30°,
∴∠C′BC=∠A′BA=30°,
∴当点A第一次落在圆上时,则点C运动的路线长为:![]() .
.
∵△ABC是三边在正方形CBA′C″上,BC边每12次回到原来位置,
2017÷12=168.08,
∴当△ABC完成第2017次旋转时,BC边共回到原来位置168次,
故答案为:![]() ,168.
,168.

【题目】某中学为了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其它四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了尚不完整的频数分布表:
类别 | 频数(人数) | 频率 |
文学 | m | 0.42 |
艺术 | 22 | 0.11 |
科普 | 66 | n |
其他 | 28 | |
合计 | 1 |
(1)表中m= ,n= ;
(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最少?
(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人?