Question

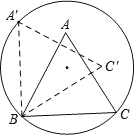
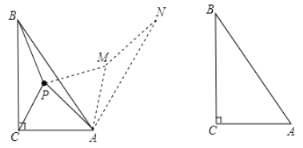
【题目】如图，在Rt△ABC中，∠C＝90°，∠B＝30°，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于M，N两点；再分别以点M，N为圆心，大于MN长为半径作圆弧，两条圆弧交于点P，作射线AP交边BC于点D．若△ABC的面积为10，则△ACD的面积为_____．

Answer 1

【答案】

【解析】

利用含30度的直角三角形三边的关系得到AC＝AB，则利用基本作图得到AD平分∠BAC，所以点D到AB、AC的距离相等，利用三角形面积公式得到S△ACD：S△ABD＝1：2，从而可计算△ACD的面积．

解：∵∠C＝90°，∠B＝30°，

∴AC＝AB，

由作法得AD平分∠BAC，

∴点D到AB的距离为CD的长，即点D到AB、AC的距离相等，

∴S△ACD：S△ABD＝AC：AB＝1：2，

∴S△ACD：S△ABC＝1：3，

∴S△ACD＝×10＝．

故答案为．