Question

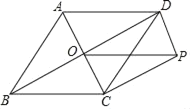
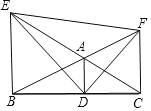
【题目】如图，从△ABC各顶点作平行线AD∥EB∥FC，各与其对边或其延长线相交于D，E，F．若△ABC的面积为1，则△DEF的面积为（　　）

A.3B.C.D.2

Answer 1

【答案】D

【解析】

根据平行线间的距离处处相等得到：△ADE和△ABD在底边AD上的高相等，△ADF和△ADC在底边AD上的高相等，△BEF和△BEC在底边BE上的高相等，所以由三角形的面积公式和图形间的面积的数量关系进行证明即可．

证明：∵AD∥BE，AD∥FC，FC∥BE，

∴△ADE和△ABD在底边AD上的高相等，△ADF和△ADC在底边AD上的高相等，△BEF和△BEC在底边BE上的高相等，

∴S△ADF＝S△ADC，S△BEF＝S△BEC，S△AEF＝S△BEF﹣S△ABE＝S△BEC﹣S△ABE＝S△ABC

∴S△DEF＝S△ADE+S△ADF+S△AEF＝S△ABD+S△ADC+S△ABC＝2S△ABC．

即S△DEF＝2S△ABC．

∵S△ABC＝1，

∴S△DEF＝2，

故选：D．