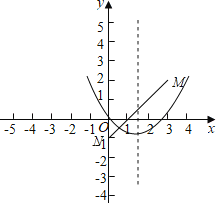Question

【题目】已知点M(3，2)，抛物线L：y＝x2﹣3x+c与x轴从左到右的交点为A，B．

（1）若抛物线L经过点M(3，2)，求抛物线L的解析式和顶点坐标；

（2）当2OA＝OB时，求c的值；

（3）直线y＝x+b经过点M，与y轴交于点N，①求点N的坐标；②若线段MN与抛物线L：y＝x2﹣3x+c有唯一公共点，直接写出正整数c的值．

Answer 1

【答案】（1）y=x2﹣3x+2，顶点坐标为(，﹣)；（2）2或﹣18；（3）①(0，﹣1)，②1和3

【解析】

（1）把点M的坐标代入抛物线解析式，利用方程求得c的值；将已得函数解析式配方，可以求得顶点坐标．

（2）设A（，0），则OB=2OA=2||，需对的正负性进行分类讨论．若＞0，则B（2，0），根据点A、B关于抛物线对称轴对称可求得的值，再把点A坐标代入抛物线解析式，解方程即求得c的值．若＜0，则B（﹣2，0），计算方法与前面一样．

（3）①利用待定系数法确定一次函数解析式，令x=0即求得点N的坐标．

②由于抛物线开口方向、大小，及对称轴固定，可把抛物线看作上下平移，再观察其与线段MN的交点情况．先联立直线MN和抛物线解析式得到关于x的一元二次方程，计算△＝0时c的值，把c的值代回方程组求得直线和抛物线此时的交点，落在线段MN上，说明c的值满足条件．把抛物线向下平移，刚好过点M时求出c的值，此时直线与抛物线由两个交点；继续往下平移抛物线，就变成只有一个交点；一直到抛物线经过点N为止，求c的值，于是得到满足条件的c的范围，再取正整数即为所求．

（1）∵抛物线L：y=x2﹣3x+c经过M（3，2）

∴9﹣9+c=2

解得：c=2．

∴y=x2﹣3x+2=（x﹣）2﹣

∴抛物线L的解析式为：y=x2﹣3x+2，顶点坐标为（，﹣）

（2）设A（，0），则OA=||，OB=2OA=2||

①若＞0，则B（2，0）

∵抛物线对称轴为直线：x=，点A、B关于对称轴对称

∴，即

解得：=1

∴A（1，0）代入抛物线解析式得：1﹣3+c=0

解得：c=2

②若＜0，则B（﹣2，0）

∴

解得：=﹣3

∴A（﹣3，0）代入抛物线解析式得：9+9+c=0

解得：c=﹣18

综上所述，c的值为2或﹣18．

（3）①∵直线y=x+b经过点M（3，2）

∴3+b=2，解得：b=﹣1

∴直线解析式为y=x﹣1

当x=0时，y=﹣1

∴点N坐标为（0，﹣1）

②联立直线MN与抛物线解析式得：

整理得：x2﹣4x+c+1=0

当直线与抛物线只有一个交点时，△=（﹣4）2﹣4（c+1）=0

解得：c=3

∴方程的解为：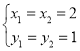

∴此时交点在线段MN上，即c=3满足“线段MN与抛物线L：y=x2﹣3x+c有唯一公共点”

当抛物线经过点M时，解得c=2，此时抛物线与线段MN有2个公共点

当抛物线往下平移到经过点N时，解得c=﹣1，此时抛物线与线段MN只有交点N

∴当﹣1≤c＜2时，抛物线与线段MN只有一个公共点

∴满足条件的正整数c的值为1和3．