题目内容
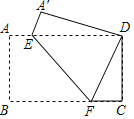
【题目】如图,在矩形ABCD中,AB=12,BC=16,将矩形ABCD沿EF折叠,使点B与点D重合,则折痕EF的长为( )
A.14B.![]() C.
C.![]() D.15
D.15
【答案】D
【解析】
设A′E=AE=x,则DE=16﹣x,在Rt△A′DE中,根据勾股定理可得x值,即AE可求,证明FC=AE,过E点作EH⊥BC于H点,则EH=AB=12,HF=BC﹣BH﹣FC,在Rt△EFH中,利用勾股定理可得EF值.
根据折叠的对称性可知AE=A′E,A′D=AB.
设AE=x,则DE=16﹣x,
在Rt△A′DE中,根据勾股定理可得DE2=A′D2+A′E2,
即(16﹣x)2=122+x2,解得x=![]() ,即AE=A′E=
,即AE=A′E=![]() .
.
根据折叠的对称性可知∠BFE=∠DFE,
又AD∥BC,
∴∠DEF=∠BFE.
∴∠DEF=∠DFE,
∴DF=DE.
又DC=A′D,
∴Rt△DFC≌Rt△DEA′(HL).
∴FC=EA′=![]() .
.
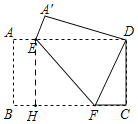
过E点作EH⊥BC于H点,则EH=AB=12,HF=BC﹣BH﹣FC=16﹣![]() ﹣
﹣![]() =9,
=9,
在Rt△EFH中,利用勾股定理可得EF=![]() .
.
故选:D.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】实验中学附近某水果超市最近新进了一批火龙果,每斤8元,为了合理定价,在第一周试行机动价格,卖出时每斤以10元为标准,超出10元的部分记为正,不足10元的部分记为负,超市记录第一周火龙果的售价情况和售出情况:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
每斤相对于标准价格(元) | +1 | -2 | +3 | -1 | +2 | +5 | -4 |
售出斤数 | 20 | 35 | 10 | 30 | 15 | 5 | 50 |
(1)这一周超市售出的火龙果单价最高的是星期 , 最高单价是 元.
(2)这一周超市总共售出火龙果多少斤?总共卖得多少元钱?
(3)这一周超市出售此种火龙果的收益如何?(盈利或亏损的钱数)