Question

【题目】已知:等边分别是上的动点，且,交于点．

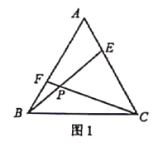
如图1,当点分别在线段和线段上时，求的度数;

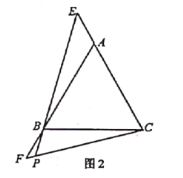
如图2,当点分别在线段和线段的延长线上时，求的度数．

Answer 1

【答案】（1）∠CPE＝60°；（2）60°

【解析】

根据等边三角形性质得出∠BAC=∠ABC=∠ACB=60°，AB=AC，根据SAS证△AFC≌△CEB，推出∠ACF＝∠CBE，根据三角形的外角性质求出即可;

同理证明△AFC≌△CEB，推出∠F＝∠E，根据三角形的外角性质求出即可．

（1）∵△ABC是等边三角形，

∴∠BAC=∠ABC=∠ACB=60°，AB=AC，

∵在AFC和△CEB中

，

∴AFC≌△CEB（SAS），

∴∠ACF＝∠CBE，

∴=∠CBE+∠BCF

=∠ACF +∠BCF

=∠ACB

=60°;

（2）同理在AFC和△CEB中

，

∴AFC≌△CEB（SAS），

∴∠F＝∠E，，

∴=∠FBP+∠F

=∠EBA +∠E

=∠BAC

=60°．