题目内容
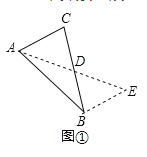
【题目】如图,在 ![]() 中,
中, ![]() ,
, ![]() 轴,垂足为
轴,垂足为 ![]() .反比例函数
.反比例函数 ![]() (
( ![]() )的图像经过点
)的图像经过点 ![]() ,交
,交 ![]() 于点
于点 ![]() .已知
.已知 ![]() ,
, ![]() .
.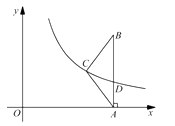
(1)若 ![]() ,求
,求 ![]() 的值;
的值;
(2)连接 ![]() ,若
,若 ![]() ,求
,求 ![]() 的长.
的长.
【答案】
(1)
解:过点C作CD⊥AB于E,
因为AC=BC,
所以AE=BE=2,
在Rt△BCE中,CE=![]() ,
,
则点C的横坐标为4-![]() ,
,
即C(![]() ,2)。
,2)。
将点C(![]() ,2)代入y=
,2)代入y=![]() ,得k=5。
,得k=5。
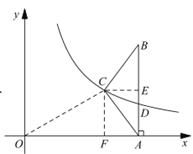
(2)
解:设A点的坐标为(m,0).
因为BD=BC=![]()
所以AD=![]()
则D,C两点的坐标分别为(m,![]() ),(m-
),(m-![]() ,2) .
,2) .
因为点D,C都在y=![]() 的图象上,
的图象上,
所以![]() ,
,
所以m=6
所以点C的坐标为(![]() ,2)
,2)
作CF⊥x轴,垂足为F.在Rt△OCF中,
OC=![]() .
.

【解析】(1)求点C的坐标,过点C作CD⊥AB于E,则AE=BE=2,由勾股定理求出CE,则求得点C的坐标,代入反比例函数即可解得;
(2)求点C的坐标,设A点的坐标为(m,0),由BD=BC=![]() ,可得D的纵坐标为AD=
,可得D的纵坐标为AD=![]() ,则D(m,
,则D(m,![]() ),C(m-
),C(m-![]() ,2) .由点D,C都在y=
,2) .由点D,C都在y=![]() 的图象上,,可求出m的值,即而求出点C的坐标,根据勾股定理即可求OC的长。
的图象上,,可求出m的值,即而求出点C的坐标,根据勾股定理即可求OC的长。
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
【题目】将正整数 1 至 1050 按一定规律排列如下表:
1 | 2 | 3 | 4 | 5 | 6 | 7 |
8 | 9 | 10 | 11 | 12 | 13 | 14 |
15 | 16 | 17 | 18 | 19 | 20 | 21 |
22 | 23 | 24 | 25 | 26 | 27 | 28 |
29 | 30 | 31 | 32 | 33 | 34 | 35 |
从表中任取一个 3 3 的方框(如表中带阴影的部分),方框中九个数的和可能是( )
A. 2025 B. 2018 C. 2016 D. 2007