题目内容
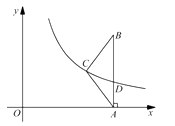
【题目】如图,二次函数 ![]() 的图像与
的图像与 ![]() 轴交于
轴交于 ![]() 、
、 ![]() 两点,与
两点,与 ![]() 轴交于点
轴交于点 ![]() ,
, ![]() .点
.点 ![]() 在函数图像上,
在函数图像上, ![]() 轴,且
轴,且 ![]() ,直线
,直线 ![]() 是抛物线的对称轴,
是抛物线的对称轴, ![]() 是抛物线的顶点.
是抛物线的顶点.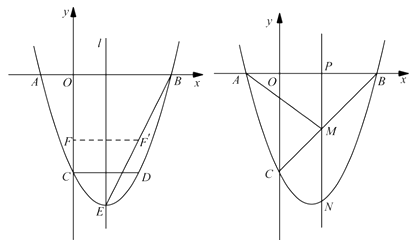
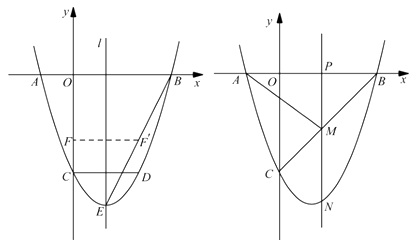
图 ① 图②
(1)求 ![]() 、
、 ![]() 的值;
的值;
(2)如图①,连接 ![]() ,线段
,线段 ![]() 上的点
上的点 ![]() 关于直线
关于直线 ![]() 的对称点
的对称点 ![]() 恰好在线段
恰好在线段 ![]() 上,求点
上,求点 ![]() 的坐标;
的坐标;
(3)如图②,动点 ![]() 在线段
在线段 ![]() 上,过点
上,过点 ![]() 作
作 ![]() 轴的垂线分别与
轴的垂线分别与 ![]() 交于点
交于点 ![]() ,与抛物线交于点
,与抛物线交于点 ![]() .试问:抛物线上是否存在点
.试问:抛物线上是否存在点 ![]() ,使得
,使得 ![]() 与
与 ![]() 的面积相等,且线段
的面积相等,且线段 ![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点 ![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
【答案】
(1)
解:∵CD⊥x轴,CD=2,
∴抛物线对称轴为直线l:x=1,
∴![]() =1,则b=-2。
=1,则b=-2。
∵OB=OC,C(0,c),
∴B点的坐标为(-c,0),
∴0=c2+2c+c,解得c=-3或c=0(舍去),
∴c=-3,
(2)
解:由(1)可得抛物线解析式为y=x2-2x-3,则E(1,-4)
设点F的坐标为(0,m),
∵对称轴为直线l:x=1,
∴点F关于直线l的对称点F的坐标为(2,m)。
∵直线BE经过点B(3,0),E(1,-4),
∴利用待定系数法可得直线BE的表达式y=2x-6,
∵点F在BE上,
∴m=2×2-6=-2,
即点F的坐标为(0,-2)。
(3)
解:存在点Q满足题意。设点P坐标为(n,0),则PA=n+1,PB=PM=3-n,PN=-n2+2n+3,
作QR⊥PN,垂足为R,
∵S△PQN=S△APM,
∴![]() (n+1)(3-n)=
(n+1)(3-n)=![]() (-n2+2n+3)QR,
(-n2+2n+3)QR,
∴QR=1。
①点Q在直线PN的左侧时,Q点的坐标为(n-1,n2-4n),R点的坐标为(n,n2-4n),N点的坐标为(n,n2-2n-3),
∴在Rt△QRN中,NQ2=1+(2n-3)2,
∴n=![]() 时,NQ取最小值1,此时Q点的坐标为(
时,NQ取最小值1,此时Q点的坐标为(![]() ,
,![]() )
)
②点Q在直线PN的右侧时,Q点的坐标为(n+1,n2-4).
同理NQ2=1+(2n-1)2,
∴n=![]() 时,NQ取最小值1,此时Q点的坐标为(
时,NQ取最小值1,此时Q点的坐标为(![]() ,
,![]() ).
).
综上所述,满足题意的点Q的坐标为(![]() ,
,![]() )和(
)和(![]() ,
,![]() )
)
【解析】(1)因为CD⊥x轴,所以C与D的纵坐标相等,即C与D关于抛物线的对称轴对称,则可得对称轴是直线l:x=1,从而由x=-![]() 代入a的值,求出b;又由OB=OC,可得B(-c,0),代入二次函数解析式,求出c的值即可;
代入a的值,求出b;又由OB=OC,可得B(-c,0),代入二次函数解析式,求出c的值即可;
(2)设点F的坐标为(0,m)关于直线x=1的对称点为(2,m),则求出BE的解析式,将(2,m)代入解出m的值即可;
(3)可设P(n,0),用n可表示出PA=n+1,PB=PM=3-n,PN=-n2+2n+3,作QR⊥PN,垂足为R,由S△PQN=S△APM , 可列出方程求出QR=1;
分类讨论点Q在直线PN的左侧和Q在直线PN的右侧时,在Rt△QRN中,由勾股定理可得NQ2=QR2+NR2,求出当n为多少时,NQ为最小值,写出相对应的Q的坐标。
【考点精析】掌握二次函数的图象和三角形的面积是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;三角形的面积=1/2×底×高.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
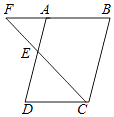
三点一测快乐周计划系列答案【题目】图1是用绳索织成的一片网的一部分,小明探索这片网的结点数(V),网眼数(F),边数(E)之间的关系,他采用由特殊到一般的方法进行探索,列表如下:
特殊网图 |
|
|
|
|
结点数(V) | 4 | 6 | 9 | 12 |
网眼数(F) | 1 | 2 | 4 | 6 |
边数(E) | 4 | 7 | 12 | ☆ |
表中“☆”处应填的数字为_____;根据上述探索过程,可以猜想V,F,E之间满足的等量关系为_____;
如图2,若网眼形状为六边形,则V,F,E之间满足的等量关系为___ .