题目内容
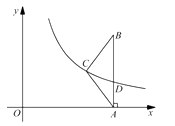
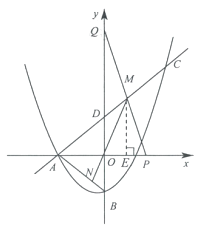
【题目】如图,抛物线 ![]() 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C ![]() 在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示).
【答案】
(1)
解:把点C(6,![]() )代入抛物线得:
)代入抛物线得:![]() =9+
=9+![]() +c.
+c.
解得c=-3.
当y=0时,![]() x2+
x2+![]() x-3=0.
x-3=0.
解得:x1=-4,x2=3.
∴A(-4,0).
设直线AC的函数表达式为:y=kx+b(k≠0).
把A(-4,0),C(6,![]() )代入得:
)代入得:
![]()
解得:![]()
∴直线AC的函数表达式为:y=![]() x+3.
x+3.
(2)
①证明:∵在Rt△AOB中,tan∠OAB=![]() =
=![]() .
.
在Rt△AOB中,tan∠OAD=![]() =
=![]() .
.
∴∠OAB=∠OAD.
∵在Rt△POQ中,M为PQ中点.
∴OM=MP.
∴∠MOP=∠MPO.
又 ∵∠MOP=∠AON.
∴∠APM=∠AON.
∴△APM∽△AON.
②解:如下图,过点M作ME⊥x轴于点E.
∵OM=MP.
∴OE=EP.
又∵点M的横坐标为m.
∴AE=m+4,AP=2m+4.
∵tan∠OAD=![]() .
.
∴cos∠EAM=cos∠OAD=![]() .
.
∴AM=![]() AE=
AE=![]() .
.
∵△APM∽△AON.
∴![]() =
=![]() .
.
∴AN=![]() =
=![]() .
.
【解析】(1)把点C(6,![]() )代入抛物线求出c的值,令y=0求出A点坐标,再用待定系数法求出直线AC的函数表达式.
)代入抛物线求出c的值,令y=0求出A点坐标,再用待定系数法求出直线AC的函数表达式.
(2)①在Rt△AOB中,tan∠OAB=![]() =
=![]() . 在Rt△AOB中,tan∠OAD=
. 在Rt△AOB中,tan∠OAD=![]() =
=![]() .从而得出∠OAB=∠OAD;在Rt△POQ中,M为PQ中点得出OM=MP.∠APM=∠AON;从而证明△APM∽△AON.
.从而得出∠OAB=∠OAD;在Rt△POQ中,M为PQ中点得出OM=MP.∠APM=∠AON;从而证明△APM∽△AON.
②如上图,过点M作ME⊥x轴于点E;由OM=MP.得出OE=EP;点M的横坐标为m;得出AE=m+4,AP=2m+4.
根据tan∠OAD=![]() .求出cos∠EAM=cos∠OAD=
.求出cos∠EAM=cos∠OAD=![]() ;再根据△APM∽△AON;得出AN=
;再根据△APM∽△AON;得出AN=![]() =
=![]() .
.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 阳光课堂同步练习系列答案
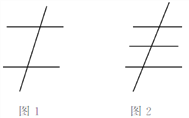
阳光课堂同步练习系列答案【题目】图1是用绳索织成的一片网的一部分,小明探索这片网的结点数(V),网眼数(F),边数(E)之间的关系,他采用由特殊到一般的方法进行探索,列表如下:
特殊网图 |
|
|
|
|
结点数(V) | 4 | 6 | 9 | 12 |
网眼数(F) | 1 | 2 | 4 | 6 |
边数(E) | 4 | 7 | 12 | ☆ |
表中“☆”处应填的数字为_____;根据上述探索过程,可以猜想V,F,E之间满足的等量关系为_____;
如图2,若网眼形状为六边形,则V,F,E之间满足的等量关系为___ .