题目内容
【题目】已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.

(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;
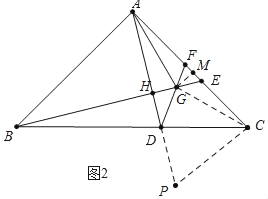
(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG.若AG平分∠CAD,求证:AH=![]() AC.
AC.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)如图1中,在AB上取一点M,使得BM=ME,连接ME.,设AE=x,则ME=BM=2x,AM=![]() x,根据AB+AE=BE,可得方程(2x+
x,根据AB+AE=BE,可得方程(2x+![]() x)+x=2,解方程即可解决问题.(2)如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.首先证明AM=MC,再证明AH=AM即可解决问题.
x)+x=2,解方程即可解决问题.(2)如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.首先证明AM=MC,再证明AH=AM即可解决问题.
本题解析:(1)如图1中,在AB上取一点M,使得BM=ME,连接ME.
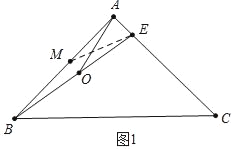
在Rt△ABE中,∵OB=OE,
∴BE=2OA=2,
∵MB=ME,
∴∠MBE=∠MEB=15°,
∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=![]() x,
x,
∵AB2+AE2=BE2,
∴(2x+![]() x)2+x2=22,
x)2+x2=22,
∴x=![]() (负根已经舍弃),
(负根已经舍弃),
∴AB=AC=(2+![]() )
)![]() ,
,
∴BC=![]() AB=
AB=![]() +1.
+1.
(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.
∵BE⊥AP,
∴∠AHB=90°,
∴∠ABH+∠BAH=90°,
∵∠BAH+∠PAC=90°,
∴∠ABE=∠PAC,
在△ABE和△CAP中,
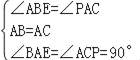 ,
,
∴△ABE≌△CAP,
∴AE=CP=CF,∠AEB=∠P,
在△DCF和△DCP中,
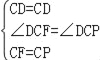 ,
,
∴△DCF≌△DCP,
∴∠DFC=∠P,
∴∠GFE=∠GEF,
∴GE=GF,∵GM⊥EF,
∴FM=ME,
∵AE=CF,
∴AF=CE,
∴AM=CM,
在△GAH和△GAM中,
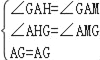 ,
,
∴△AGH≌△AGM,
∴AH=AM=CM=![]() AC.
AC.

 名校课堂系列答案
名校课堂系列答案