题目内容
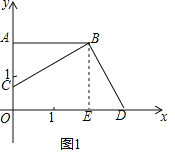
【题目】如图,在平面直角坐标系xOy中,点A在y轴上,点B是第一象限的点,且AB⊥y轴,且AB=OA,点C是线段OA上任意一点,连接BC,作BD⊥BC,交x轴于点D.
(1)依题意补全下图;
(2)用等式表示线段OA,AC与OD之间的数量关系,并证明;
(3)连接CD,作∠CBD的平分线,交CD边于点H,连接AH,求∠BAH的度数.

【答案】(1)见解析;(2)OA+AC=OD,见解析;(3)45°
【解析】
(1)根据题意画出图形即可;
(2)过B作BE⊥x轴于E,则四边形AOEB是矩形,根据矩形的想知道的BE=AO,∠ABE=90°,等量代换得到AB=BE推出△ABC≌△EBD,根据全等三角形的性质得到AC=DE,等量代换即可得到结论;
(3)根据全等三角形的性质得到BC=BD,推出△BCD是等腰直角三角形,于是得到∠BCD=45°,根据等腰三角形的性质得到∠BHC=90°,过H作HN⊥OA,HM⊥AB,证明△CNH≌△BHM,可得出HN=HM,则AH平分∠CAB,可得到结论.
解:(1)如图1所示,
(2)OA+AC=OD,
如图1,过B作BE⊥x轴于E,
则四边形AOEB是矩形,
∴BE=AO,∠ABE=90°,
∵AB=AO,
∴AB=BE,
∵BD⊥BC,
∴∠CBD=90°,
∴∠ABC=∠DBE,
在△ABC与△BDE中,
 ,
,
∴△ABC≌△EBD(ASA),
∴AC=DE,
∵OE=AB=OA,
∴AO+AC=OD;
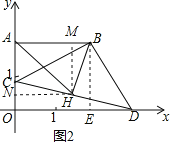
(3)如图2,由(1)知:△ABC≌△EBD,
∴BC=BD,
∵BD⊥BC,
∴△BCD是等腰直角三角形,
∴∠BCD=45°,
∵BH平分∠CBD,
∴∠BHC=90°,
∵∠BAO=90°,
过H作HN⊥OA,HM⊥AB,
∴四边形ANMH是矩形,
∴∠NHM=90°,
∴∠NHC=∠MHB,
∴△CNH≌△BHM(AAS),
∴HN=HM,
∴AH平分∠CAB,
∴∠BAH=45°.

 名校课堂系列答案
名校课堂系列答案




