题目内容
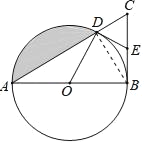
【题目】如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O交AB于点D,点E为BC的中点,连接OD、DE.
(1)求证:OD⊥DE;
(2)若∠BAC=30°,AB=12,求阴影部分的面积.

【答案】(1)详见解析;(2)12π﹣9![]() .
.
【解析】
(1)连接DB,根据圆周角定理、直角三角形的性质证明;
(2)根据扇形面积公式计算即可.
(1)证明:连接DB.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=90°,
∵点E是BC的中点,
∴DE=CE=![]() BC,
BC,
∴∠EDC=∠C,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠A+∠C=90°,
∴∠ADO+∠EDC=90°,
∴∠ODE=90°,
∴OD⊥DE;
(2)∵AB=12,∠BAC=30°,
∴AD=6![]() ,
,
阴影部分的面积=![]() ﹣
﹣![]() ×6×3
×6×3![]()
=12π﹣9![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目