题目内容
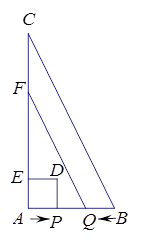
如图,ABC中,∠A=90º,AB=2㎝,AC=4㎝,动点P从点A出发,沿AB方向以1㎝/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1㎝s的速度向带你A运动,当点P到达点B时,P、Q两点同时停止运动.以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F,设点P的运动时间为t s,正方形APDE和梯形BCFQ重合部分的面积为S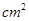 .
.
(1)当t= s时,点P与点Q重合;
(2)当t= s时,点D在QF上;
(3)当点P在Q、B两点之间(不包括Q、B两点)时,求S与t之间的函数关系式.
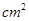 .
.
(1)当t= s时,点P与点Q重合;
(2)当t= s时,点D在QF上;
(3)当点P在Q、B两点之间(不包括Q、B两点)时,求S与t之间的函数关系式.
(1)1,(2) ;(3)1<
;(3)1<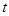 ≤
≤ 时,S=
时,S=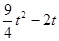 ;当
;当 <
<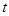 <2时S=
<2时S=
 ;(3)1<
;(3)1<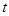 ≤
≤ 时,S=
时,S=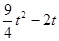 ;当
;当 <
<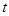 <2时S=
<2时S=
试题分析:(1)当两点重合时,AP=BQ=t,且AP+BQ=AB=2
即2t=2,t=1
(2)当点D在QF上时,此时AP=BQ=1
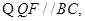

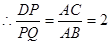
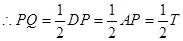
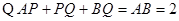

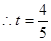
(3)由题意可知,当P在Q,B之间时,可分一下两种情况
当
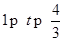 ,此时重合部分是题型
,此时重合部分是题型即AP=BQ=t,PQ=AP-AQ=2t-2
可知
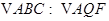
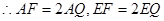

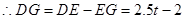

当
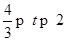
此时易得
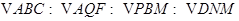
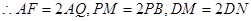
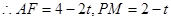
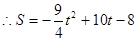
点评:此题将用待定系数法求二次函数解析式、动点问题和最小值问题相结合,有较大的思维跳跃,考查了同学们的应变能力和综合思维能力,是一道好题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.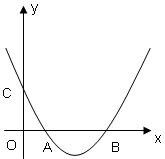
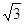 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.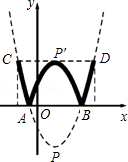
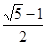 .请你计算这个“W”图案的高与宽的比到底是多少?
.请你计算这个“W”图案的高与宽的比到底是多少? 的图象与
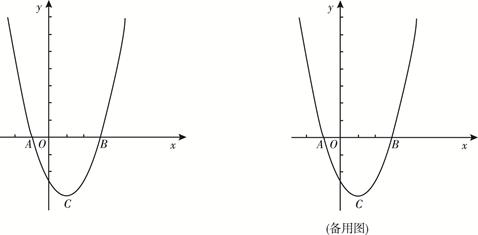
的图象与 轴交于
轴交于 (-1,0)、
(-1,0)、 (3,0)两点, 顶点为
(3,0)两点, 顶点为 .
.
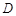 为点
为点 作直线
作直线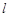 :
: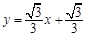 交BD于点E,过点
交BD于点E,过点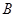 作直线
作直线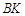 ∥
∥ 交直线
交直线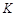 点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;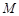 、
、 分别为直线
分别为直线 、
、 、
、 ,求
,求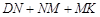 和的最小值.
和的最小值. 上.
上.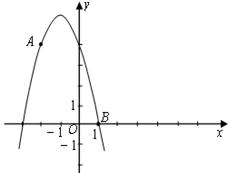
 、n;
、n;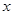 轴上找点D,使得以点B′、C、D为顶点的三角形与
轴上找点D,使得以点B′、C、D为顶点的三角形与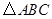 相似.
相似. 的图像与y轴的交点坐标是( ).
的图像与y轴的交点坐标是( ). x2﹣7x+
x2﹣7x+ ,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )
,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( ) 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
. 的取值范围;(2)当
的取值范围;(2)当 时,求
时,求