题目内容
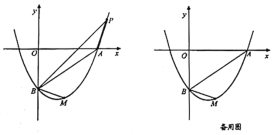
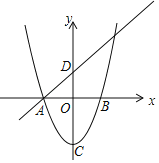
【题目】如图,已知抛物线y=x2﹣4与x轴交于点A,B(点A位于点B的左侧),C为顶点,直线y=x+m经过点A,与y轴交于点D.
(1)求线段AD的长;
(2)沿直线AD方向平移该抛物线得到一条新拋物线,设新抛物线的顶点为C',若点C'在反比例函数![]() (x<0)的图象上.求新抛物线对应的函数表达式.
(x<0)的图象上.求新抛物线对应的函数表达式.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)通过解方程求出点A的坐标,由此进一步求出![]() 的值,从而得出D点坐标,最后根据勾股定理计算即可;
的值,从而得出D点坐标,最后根据勾股定理计算即可;
(2)设新抛物线对应的函数表达式为![]() ,根据题意求出直线CC′的解析式,由此进一步求出C′坐标,据此再加以计算求解即可.
,根据题意求出直线CC′的解析式,由此进一步求出C′坐标,据此再加以计算求解即可.
(1)由![]() 得,
得,![]() ,
,![]() ,
,
∵点A位于点B的左侧,
∴A(![]() ,0),
,0),
∵直线![]() 经过点A,
经过点A,
∴![]() ,
,
∴m=2,
∴点D的坐标为(0,2),
∴AD=![]() ;
;
(2)设新抛物线对应的函数表达式为:![]() ,
,
∴C'(m,n),
∵CC′平行于直线AD,且经过C(0,4),
∴直线CC′的解析式为:![]() ,
,
∵点C'在反比例函数![]() (
(![]() )的图象上,
)的图象上,
∴![]() ,
,
∴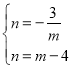 ,
,
解得:![]() 或
或![]() ,
,
∴新抛物线对应的函数表达式为![]() 或
或![]() ,
,
∴新抛物线对应的函数表达式为:![]() 或
或![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目