题目内容
【题目】如图，
中，
．
． 将
绕点
顺时针旋转60°到点
，点
与点关于直线
对称，连接
，
，
．
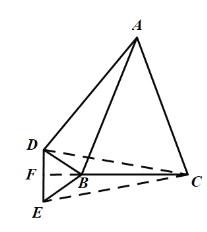
(1)依题意补全图形：
(2)判断
的形状，并证明你的结论；
(3)请问在直线上是否存在点
．使得
恒成立若存在，请用文字描述出点的准确位置，并画图证明；若不存在，请说明理由．
【答案】（1）图见解析；（2）
是等边三角形，理由见解析；（3）存在，点P是在将
绕点C顺时针旋转60°得到
，直线
与直线
的交点，图和理由见解析．
【解析】
（1）根据题意画出图形即可；
（2）首先利用垂直平分线的性质得出
，然后根据旋转的性质有
是等边三角形，然后利用等边三角形，等腰三角形的性质和三角形内角和定理得出
，从而可证
，则有
，从而可证是等边三角形；
（3）将绕点C顺时针旋转60°得到，延长交直线于点P，连接
，先利用旋转的性质得出
是等边三角形，然后通过等量代换得出
，从而可证
，则
，再通过等腰三角形的性质和角度之间的关系得出
，又因为
，
，则有
．
（1）如图，
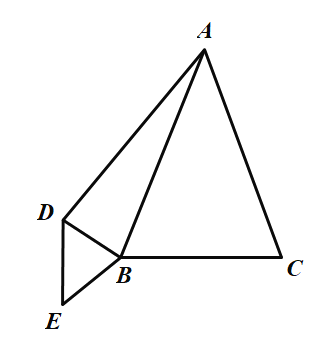
（2）是等边三角形，理由如下：
连接CD,CE，延长CB交DE于点F，
∵点
与点
关于直线
对称，
∴CF垂直平分DE，
∴ ．
由旋转可知，
，
是等边三角形，
，
．
，
，
，
，
，
．
在
和
中，
，
，
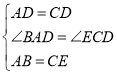
∴是等边三角形；
（3）存在，点P是在将绕点C顺时针旋转60°得到，直线与直线的交点，理由如下：
将绕点C顺时针旋转60°得到，延长交直线于点P，连接，如图，
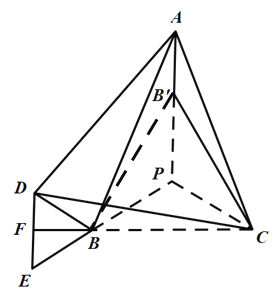
由（2）可知是等边三角形，
，
，
．
由旋转可知，
，
∴是等边三角形，
，
，
．
在
和
中，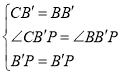
．
，
，
，
，
．
，
，
∴直线BE上存在一点P，使得，点P是在将绕点C顺时针旋转60°得到，直线与直线的交点．
练习册系列答案
相关题目
