题目内容
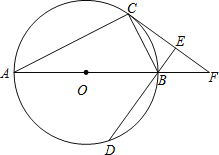
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:
①若AB=4,当OB=BF时,BE=______;
②当∠CAB的度数为______时,四边形ACFD是菱形.
【答案】(1)证明见解析;(2)①1;②30°.
【解析】
(1)连结OC,如图,由于∠OAC=∠OCA,则根据三角形外角性质得∠BOC=2∠OAC,而∠ABD=2∠BAC,所以∠ABD=∠BOC,根据平行线的判定得到OC∥BD,再CE⊥BD得到OC⊥CE,然后根据切线的判定定理得CF为⊙O的切线;
(2)①由平行线分线段成比例可得![]() ,即可求BE的长;
,即可求BE的长;
②根据三角形的内角和得到∠F=30°,根据等腰三角形的性质得到AC=CF,连接AD,根据平行线的性质得到∠DAF=∠F=30°,根据全等三角形的性质得到AD=AC,由菱形的判定定理即可得到结论.
证明:(1)连结OC,如图,

∵OA=OC,
∴∠OAC=∠OCA,
∴∠BOC=∠A+∠OCA=2∠OAC,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)①∵AB=4,
∴OB=BF=OC=2,
∴OF=4,
∵BE∥OC,
∴![]() ,
,
∴BE=1,
故答案为:1;
②当∠CAB的度数为30°时,四边形ACFD是菱形,
理由:∵∠CAB=30°,
∴∠COF=60°,
∴∠F=30°,
∴∠CAB=∠F,
∴AC=CF,
连接AD,
∵AB是⊙O的直径,
∴AD⊥BD,
∴AD∥CF,
∴∠DAF=∠F=30°,
在△ACB与△ADB中,
 ,
,
∴△ACB≌△ADB(AAS),
∴AD=AC,
∴AD=CF,
∵AD∥CF,
∴四边形ACFD是菱形.
故答案为:30°.

 阅读快车系列答案
阅读快车系列答案【题目】某中学对本校学生每天完成作业所用时间的情况进行抽样调查,随机调查了九年级部分学生每天完成作业所用的时间,并把统计结果制作成如图所示的频数分布直方图(时间取整数,图中从左至右依次为第一、二、三、四、五组)和扇形统计图.请结合图中信息解答下列问题.
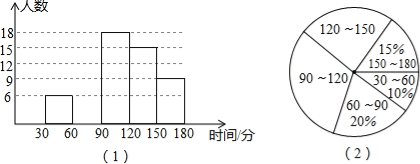
(1)本次调查的学生人数为 人;
(2)补全频数分布直方图;
(3)根据图形提供的信息判断,下列结论正确的是 (只填所有正确结论的代号);
A.由图(1)知,学生完成作业所用时间的中位数在第三组内 |
B.由图(1)知,学生完成作业所用时间的众数在第三组内 |
C.图(2)中,90~120数据组所在扇形的圆心角为108° |
D.图(1)中,落在第五组内数据的频率为0.15 |
(4)学生每天完成作业时间不超过120分钟,视为课业负担适中.根据以上调查,估计该校九年级560名学生中,课业负担适中的学生约有多少人?