题目内容
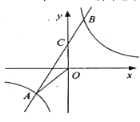
【题目】如图所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点Q.设点Q的坐标为(x,y),则y关于x的函数关系式是_______________

【答案】![]()
【解析】
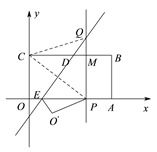
如图,连接CQ、CP,设PQ与BC的交点为点M,
由已知条件可得:PM=OC=AB=2,CM=x,PQ=y,∠QMC=90°,
∴QM=PQ-PM=y-2,
∵点C和点P关于直线QE对称,
∴直线QE是线段CP的垂直平分线,
∴CQ=PQ=y,
又∵再Rt△QCM中:![]() ,
,
∴![]() ,
,
化简整理得:![]() .
.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案【题目】我市雷雷服饰有限公司生产了一款夏季服装,通过实验商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量![]() (百件)与时间
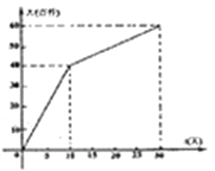
(百件)与时间![]() (
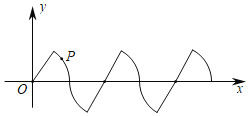
(![]() 为整数,单位:天)的关系如下图所示.
为整数,单位:天)的关系如下图所示.
时间 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量 | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为![]() (百件),求
(百件),求![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 为何值时,日销售总量
为何值时,日销售总量![]() 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.
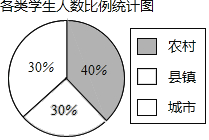
【题目】某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
各类学生成绩人数比例统计表
等第 人数 类别 | A | B | C | D |
农村 | 200 | 240 | 80 | |
县镇 | 290 | 132 | 130 | |
城市 | 240 | 132 | 48 |
(注:等第A、B、C、D分别代表优秀、良好、合格、不合格)
(1)请将上面表格中缺少的三个数据补充完整;
(2)若该市九年级共有15000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.