题目内容
【题目】我市雷雷服饰有限公司生产了一款夏季服装,通过实验商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
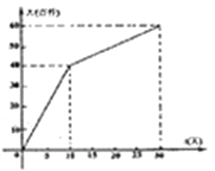
(![]() 为整数,单位:天)的关系如下图所示.
为整数,单位:天)的关系如下图所示.
时间 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量 | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为![]() (百件),求
(百件),求![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 为何值时,日销售总量
为何值时,日销售总量![]() 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.
【答案】(1)y1=﹣![]() t2+6t(0≤t≤30,且为整数);(2)
t2+6t(0≤t≤30,且为整数);(2)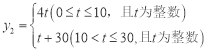 ;(3)当0≤t≤10时,y=
;(3)当0≤t≤10时,y=![]() t2+6t+4t;当10<t≤30时,y=
t2+6t+4t;当10<t≤30时,y=![]() t2+6t+t+30.当t=17或18时,y最大=91.2(百件).
t2+6t+t+30.当t=17或18时,y最大=91.2(百件).
【解析】
试题分析:(1)根据观察可设y1=at2+bt+c,将(0,0),(5,25),(10,40)代入即可得到结论;
(2)当0≤t≤10时,设y2=kt,求得y2与t的函数关系式为:y2=4t,当10≤t≤30时,设y2=mt+n,将(10,40),(30,60)代入得到y2与t的函数关系式为:y2=k+30,
(3)依题意得y=y1+y2,当0≤t≤10时,得到y最大=80;当10<t≤30时,得到y最大=91.2,于是得到结论.
试题解析:(1)根据观察可设y1=at2+bt+c,将(0,0),(5,25),(10,40)代入得:
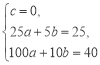 ,解得
,解得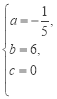 ,
,
∴y1与t的函数关系式为:y1=﹣![]() t2+6t(0≤t≤30,且为整数);
t2+6t(0≤t≤30,且为整数);
(2)当0≤t≤10时,设y2=kt,
∵(10,40)在其图象上,∴10k=40,∴k=4,
∴y2与t的函数关系式为:y2=4t,
当10≤t≤30时,设y2=mt+n,
将(10,40),(30,60)代入得![]() ,解得
,解得![]() ,
,
∴y2与t的函数关系式为:y2=t+30,
综上所述,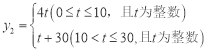 ;
;
(3)依题意得y=y1+y2,当0≤t≤10时,y=![]() t2+6t+4t=
t2+6t+4t=![]() t2+10t=
t2+10t=![]() (t﹣25)2+125,
(t﹣25)2+125,
∴t=10时,y最大=80;
当10<t≤30时,y=![]() t2+6t+t+30=
t2+6t+t+30=![]() t2+7t+30=
t2+7t+30=![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵t为整数,∴t=17或18时,y最大=91.2,
∵91.2>80,∴当t=17或18时,y最大=91.2(百件).