题目内容
【题目】如图，在平行四边形ABCD中，∠ABC的平分线BF分别与AC、AD交于点E、F．
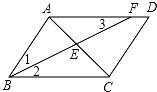
（1）求证：AB＝AF；
（2）当AB＝3，BC＝4时，求
的值．
【答案】（1）见解析；（2）
.
【解析】
（1）只要根据平行线的性质和角平分线的定义即可得到∠1＝∠3，进而可得结论；
（2）易证△AEF∽△CEB，于是AE：CE＝AF：BC，然后结合（1）的结论即可求出AE：EC，进一步即得结果.
（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，∴∠2＝∠3，
∵BF平分∠ABC，∴∠1＝∠2，
∴∠1＝∠3，
∴AB＝AF；
（2）解：∵四边形ABCD是平行四边形，∴AD∥BC，
∴△AEF∽△CEB，∴AE：CE＝AF：BC，
∵AF＝AB＝3，BC＝4，
∴AE：EC＝3：4，
∴．
练习册系列答案
相关题目
