Question

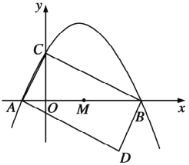
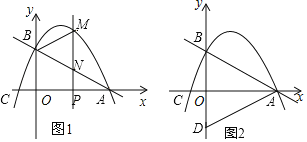
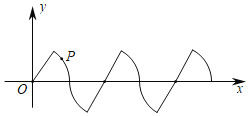
【题目】如图所示，在平面直角坐标系中，若干个半径为2个单位长度，圆心角为60°的扇形组成一条连续的曲线，点P从原点O出发，沿这条曲线向右上下起伏运动，点在直线上的速度为每秒2个单位长度，点在弧线上的速度为每秒个单位长度，则第2018秒时，点P的坐标是_____．

Answer 1

【答案】（2018，0）．

【解析】

设第n秒运动到Pn（n为自然数）点，根据点P的运动规律找出部分Pn点的坐标，根据坐标的变化找出变化规律“P4n+1（4n+1，），P4n+2（4n+2，0），P4n+3（4n+3，﹣），P4n+4（4n+4，0）”，依此规律即可得出结论．

设第n秒运动到Pn（n为自然数）点，

观察，发现规律：P1（1，），P2（2，0），P3（3，﹣），P4（4，0），P5（5，），…，

∴P4n+1（4n+1，），P4n+2（4n+2，0），P4n+3（4n+3，﹣），P4n+4（4n+4，0），

∵2018＝4×504+2，

∴P2018为（2018，0），

故答案为：（2018，0）．