Question

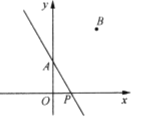
【题目】如图，已知正方形的边长为4，边在轴上，边在轴上，点是轴上一点，坐标为，点为的中点，连接.

(1)点的坐标为;

(2)判断的形状，并证明你的结论.

Answer 1

【答案】(1)； (2) 为直角三角形.

【解析】

（1）利用正方形的性质得到BC=BA，然后利用第一象限点的坐标特征写出B点坐标；

（2）先利用勾股定理分别计算出DE、BE、BD，然后利用勾股定理的逆定理可证明△BDE为直角三角形.

（1）∵正方形ABCO的边长为4，

∴BC=BA=4，

∴B点坐标为（4，4）；

故答案为（4，4）；

（2）△BDE为直角三角形．理由如下：

∵D（1，0），点E为OC的中点，

∴OE=CE=2，OD=1，

∴AD=3，

∴DE2=OD2+OE2=1+4=5，BE2=CE2+BE2=4+16=20，DB2=AD2+AB2=9+16=25，

∵5+20=25，

∴DE2+BE2=DB2，

∴△BDE为直角三角形，∠BED=90°；