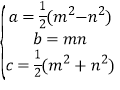Question

【题目】在平面直角坐标系中，对于任意三点的“矩面积”，给出如下定义:“水平底”为任意两点横坐标差的最大值，“铅垂高”为任意两点纵坐标差的最大值，则“矩面积”.

例如:三点坐标分别为，则“水平底”，“铅垂高”，“矩面积”.

(1)已知点.

①若三点的“矩面积”为12，求点的坐标;

②求三点的“矩面积”的最小值.

(2)已知点，其中.若三点的“矩面积”为8，求的取值范围.

Answer 1

【答案】(1)①时，；时，；②；(2) .

【解析】

（1）①首先由题意可得：a=4，然后分别从：当t＞2时，h=t-1，当t＜1时，h=2-t，去分析求解即可求得答案；

②首先根据题意得：h的最小值为：1，继而求得A，B，P三点的“矩面积”的最小值．

（2）由E，F，M三点的“矩面积”的最小值为8，可得a=4，h=2，即可得．继而求得m的取值范围．

（1）①由题意：a=4．

当t＞2时，h=t-1，

则4（t-1）=12，可得t=4，故点P的坐标为（0，4）；

当t＜1时，h=2-t，

则4（2-t）=12，可得t=-1，故点P的坐标为（0，-1）；

②∵根据题意得：h的最小值为：1，

∴A，B，P三点的“矩面积”的最小值为4；

故答案为：4；

（2）∵E，F，M三点的“矩面积”为8，

∴a=4，h=2，

∴．

∴0≤m≤．

∵m＞0，

∴0＜m≤．