题目内容
到高中时,我们将学习虚数i,(i叫虚数单位).规定i2=-1,
如-2=2×(-1)=(±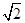 )2·i2=(±
)2·i2=(±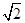 i)2,那么x2=-2的根就是:x1=
i)2,那么x2=-2的根就是:x1=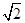 i,x2=-
i,x2=-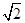 i.试求方程x2+2x+3=0的根.
i.试求方程x2+2x+3=0的根.
如-2=2×(-1)=(±
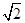 )2·i2=(±
)2·i2=(±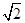 i)2,那么x2=-2的根就是:x1=
i)2,那么x2=-2的根就是:x1=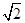 i,x2=-
i,x2=-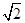 i.试求方程x2+2x+3=0的根.
i.试求方程x2+2x+3=0的根.x1=-1+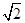 i,x2=-1-
i,x2=-1-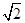 i
i
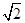 i,x2=-1-
i,x2=-1-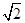 i
ix2+2x+3=0,(5分)
x2+2x+1=-2,
(x+1)2=-2,x+1=±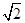 i;
i;
x=-1±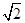 i,
i,
所以x1=-1+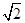 i,x2=-1-
i,x2=-1-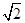 i.(15分)
i.(15分)
本题将虚数和方程结合起来求虚根,可以用配方法解一元二次方程,首先将常数项移到等号的右侧,将等号左右两边同时加上一次项系数一半的平方,即可将等号左边的代数式写成完全平方形式.
x2+2x+1=-2,
(x+1)2=-2,x+1=±
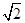 i;
i;x=-1±
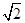 i,
i,所以x1=-1+
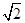 i,x2=-1-
i,x2=-1-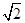 i.(15分)
i.(15分)本题将虚数和方程结合起来求虚根,可以用配方法解一元二次方程,首先将常数项移到等号的右侧,将等号左右两边同时加上一次项系数一半的平方,即可将等号左边的代数式写成完全平方形式.

练习册系列答案
相关题目
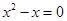 时,只得出一个根x=1,则被漏掉的一个根是
时,只得出一个根x=1,则被漏掉的一个根是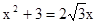 (2)
(2)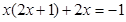
 ,按此计算,一台大型机械设备加工时的实际耗油量为
,按此计算,一台大型机械设备加工时的实际耗油量为 千克。某企业原先一台大型机械设备加工时润滑用油量为90千克,用油的重复利用率为60%。该企业进行了技术革新,发现革新后润滑用油量每减少1千克,用油量的重复利用率将增加2%。这样加工一台大型机械设备的实际耗油量下降到16千克。求:
千克。某企业原先一台大型机械设备加工时润滑用油量为90千克,用油的重复利用率为60%。该企业进行了技术革新,发现革新后润滑用油量每减少1千克,用油量的重复利用率将增加2%。这样加工一台大型机械设备的实际耗油量下降到16千克。求: 有两个不相等的实数根,则k的取值范围是 .
有两个不相等的实数根,则k的取值范围是 . (用配方法);
(用配方法);