题目内容
【题目】如图,![]() ,点
,点![]() 分别在
分别在![]() 直线上,点
直线上,点![]() 为两平行线内部一点
为两平行线内部一点

(1)如图1,![]() 角平分线交于点N,若
角平分线交于点N,若![]() 等于
等于![]() ,求
,求![]() 的度数
的度数
(2)如图2,点G为直线![]() 上一点,且
上一点,且![]() ,延长GM交直线AB于点Q,点P为MG上一点,射线
,延长GM交直线AB于点Q,点P为MG上一点,射线![]() 相交于点H,满足
相交于点H,满足![]() ,设
,设![]() ,求
,求![]() 的度数(用
的度数(用![]() 的代数式表示)
的代数式表示)
【答案】(1)115°;(2)∠H=60°-![]() α.
α.
【解析】
(1)过M作ME∥AB,利用平行线的性质以及角平分线的定义计算即可.
(2)如图②中设∠BEH=x,∠PFG=y,则∠BEM=3x,∠MFG=3y,设EH交CD于K.证明∠H=x-y,求出x-y即可解决问题.
解:(1)过M作ME∥AB,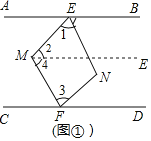
∵AB∥CD,
∴ME∥CD,
∴∠BEM+∠2=∠DFM+∠4=180°,
∴∠BEM=180°-∠2,∠DFM=180°-∠4,
∵EN,FN分别平分∠MEB和∠DFM,
∴∠1=![]() ∠BEM,∠3=
∠BEM,∠3=![]() ∠DFM,
∠DFM,
∴∠1+∠3=![]() (180°-∠2)+
(180°-∠2)+![]()
(180°-∠4)=180°-![]() (∠2+∠4)=180°-
(∠2+∠4)=180°-![]() ×130°=115°,
×130°=115°,
∴∠ENF=360°-∠1-∠3-∠EMF=360°-115°-130°=115°;
(2)如图②中设∠BEH=x,∠PFG=y,则∠BEM=3x,∠MFG=3y,设EH交CD于K.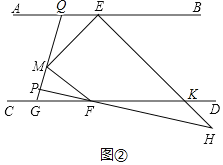
∵AB∥CD,
∴∠BEH=∠DKH=x,
∵∠PFG=∠HFK=y,∠DKH=∠H+∠HFK,
∴∠H=x-y,
∵∠EMF=∠MGF=α,∠BQG+∠MGF=180°,
∴∠BQG=180°-α,
∵∠QMF=∠QME+∠EMF=∠MGF+∠MFG,
∴∠QME=∠MFG=3y,
∵∠BEM=∠QME+∠MQE,
∴3x-3y=180°-α,
∴x-y=60°-![]() α,
α,
∴∠H=60°-![]() α.
α.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目