Question

【题目】如图，已知Rt△ABC中，∠C=90°，∠BAC=30°，点D为边BC上的点，连接AD，∠BAD=α，点D关于AB的对称点为E，点E关于AC的对称点为G，线段EG交AB于点F，连接AE，DE，DG，AG．

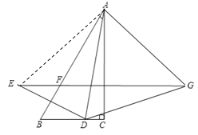
（1）依题意补全图形；

（2）求∠AGE的度数（用含α的式子表示）；

（3）猜想：线段EG与EF，AF之间是否存在一个数量关系？若存在，请写出这个数量关系并证明；若不存在，请说明理由．

Answer 1

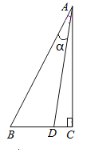
【答案】（1）见解析；（2）∠AGE=60°－α；（3）EG=2EF+AF，见解析

【解析】

（1）根据题意和轴对称的性质，补全图形即可；

（2）连接AE，根据对称的性质可得AB为ED的垂直平分线，AC为EG的垂直平分线，然后根据垂直平分线的性质可得AE=AG=AD，即可求出∠EAC和∠EAG，然后根据等边对等角和三角形的内角和定理即可求出结论；

（3）在FG上截取NG=EF，连接AN，利用SAS即可证出△AEF≌△AGN，从而得出AF=FN，即可得出结论．

解：（1）补全图形：如图所示．

（2）连接AE

由对称性可知，AB为ED的垂直平分线，AC为EG的垂直平分线．

∴AE=AG=AD．

∴∠AEG=∠AGE，∠BAE=∠BAD=α．

∴∠EAC=∠BAC+∠BAE=30°＋α．

∴∠EAG=2∠EAC=60°＋2α．

∴∠AGE==60°－α

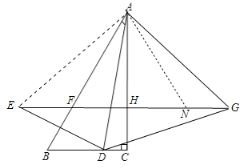
（3）存在，即：EG=2EF+AF．

证明：在FG上截取NG=EF，连接AN．

∵AE=AG，

∴∠AEG=∠AGE．

∵EF=GN

∴△AEF≌△AGN．

∴AF=AN．

∵∠EAF=α，∠AEG=60°－α．

∴∠AFN=∠EAF ＋∠AEG=60°．

∴△AFN为等边三角形．

∴AF=FN．

∴EG=EF+FN+NG=2EF+AF．