题目内容
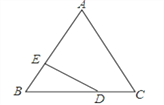
【题目】如图,△ABC中AB=6,AC=8,D是BC边上一动点,DE∥AC交AB于E,DF∥AB交AC于F.
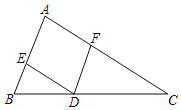
(1)若BC=10,判断四边形AEDF的形状并证明;
(2)在(1)的条件下,若四边形AEDF是正方形,求BD的长;
(3)若∠BAC=60°,四边形AEDF是菱形,则BD= .
【答案】(1)四边形AEDF是矩形,理由见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)首先判定平行四边形,然后证明一个内角为90°,从而判定矩形;
(2)首先根据面积法求得DE的长,然后利用勾股定理求得BD的长即可;
(3)根据面积求得BD:CD=3:4,然后求得BD的长.
解:(1)AEDF是矩形,理由如下
∵AB2+AC2=62+82=BC2=102,
由勾股定理得∠BAC=90°
∵DE∥AF、DF∥AE,
∴四边形AEDF是平行四边形,
又∵∠BAC=90°,
∴四边形AEDF是矩形;
(2)由(1)得,当DE=DF时,四边形AEDF是正方形.
设DE=DF=x,建立面积方程S△ABC=![]() ACBD=
ACBD=![]() DE(AB+AC);
DE(AB+AC);
即:![]() ×6×8=
×6×8=![]() x×(6+8),
x×(6+8),
解得:x=![]() ,
,
∴DE=AE=![]() ,BE=AB﹣AE=
,BE=AB﹣AE=![]() ,
,
在Rt△DEB中,由勾股定理得:BD=![]() =
=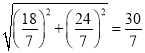 ;
;
(3)依题意得,当AD是∠BAC角平分线时,四边形AEDF是菱形.
点B作AC的垂线段交于点G,
又∵∠BAG=60°,
∴AG=3,CG=5,BG=![]() ,
,
由勾股定理得:BC=![]() ,
,
∵AD平分∠BAC,
∴S▲ABD:S▲ACD=AB:AC=BD:CD,
即BD:CD=3:4.
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目