题目内容
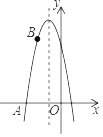
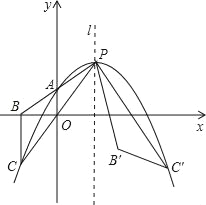
【题目】如图,抛物线y=a(x﹣m﹣1)2+2m(其中m>0)与其对称轴l相交于点P.与y轴相交于点A(0,m)连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC将△PBC绕点P逆时针旋转,使点C落在抛物线上,设点C、B的对应点分别是点B′和C′.
(1)当m=1时,该抛物线的解析式为: .
(2)求证:∠BCA=∠CAO;
(3)试问:BB′+BC﹣BC′是否存在最小值?若存在,求此时实数m的值,若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+x+1;(2)见解析;(3)BB′+BC﹣BC′存在最小值,m=1+
x2+x+1;(2)见解析;(3)BB′+BC﹣BC′存在最小值,m=1+![]() .
.
【解析】
(1)把点A的坐标代入二次函数表达式得:m=a(﹣m﹣1)2+2m,解得:a=﹣![]() ,把m=1代入上式,即可求解;
,把m=1代入上式,即可求解;
(2)求出点B、C的坐标,即可求解;
(3)当点B′落在BC′所在的直线时,BB′+BC﹣BC′存在最小值,证△BAO∽△POD,即可求解.
解:(1)把点A的坐标代入二次函数表达式得:m=a(﹣m﹣1)2+2m,解得:a=﹣![]() ,
,
则二次函数的表达式为:y=﹣![]() (x﹣m﹣1)2+2m…①,
(x﹣m﹣1)2+2m…①,
则点P的坐标为(m+1,2m),点A的坐标为(0,m),
把m=1代入①式,整理得:y=﹣![]() x2+x+1,
x2+x+1,
故:答案为:y=﹣![]() x2+x+1;
x2+x+1;
(2)把点P、A的坐标代入一次函数表达式:y=kx+b得:
![]() ,解得:
,解得: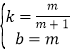 ,
,
则直线PA的表达式为:y=![]() x+m,
x+m,
令y=0,解得:x=﹣m﹣1,即点B坐标为(﹣m﹣1,0),
同理直线OP的表达式为:y=![]() x…②,
x…②,
将①②联立得:a(x﹣m﹣1)2+2m﹣![]() x=0,其中a=﹣
x=0,其中a=﹣![]() ,
,
该方程的常数项为:a(m+1)2+2m,
由韦达定理得:x1x2=xCxP=![]() =
=![]() =﹣(m+1)2,
=﹣(m+1)2,
其中
则xC=﹣m﹣1=xB,
∴BC∥y轴,
∴∠BCA=∠CAO;
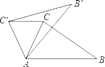
(3)如图当点B′落在BC′所在的直线时,BB′+BC﹣BC′存在最小值,

设:直线l与x轴的交点为D点,连接BB′、CC′,
∵点C关于l的对称点为C′,
∴CC′⊥l,而OD⊥l,∴CC′∥OD,∴∠POD=∠PCC′,
∵∠PB′C′+∠PB′B=180°,
△PB′C′由△PBC旋转而得,
∴∠PBC=∠PB′C′,PB=PB′,∠BPB′=∠CPC′,
∴∠PBC+∠PB′B=180°,
∵BC∥AO,
∴∠ABC+∠BAO=180°,
∴∠PB′B=∠BAO,
∵PB=PB′,PC=PC′,
∴∠PB′B=∠PBB′=![]() ,
,
∴∠PCC′=∠PC′C=![]() ,
,
∴∠PB′B=∠PCC′,
∴∠BAO=∠PCC′,
而∠POD=∠PCC′,
∴∠BAO=∠POD,
而∠POD=∠BAO=90°,
∴△BAO∽△POD,
∴![]() ,
,
将BO=m+1,PD=2m,AO=m,OD=m+1代入上式并解得:
m=1+![]() (负值已舍去).
(负值已舍去).