题目内容
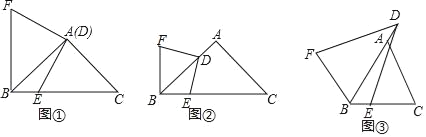
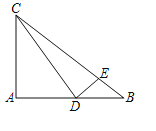
【题目】如图,四边形 ABCD 中, AC 平分 ∠ DAB , ∠ ADC= ∠ ACB=90° , E 为 AB 的中点,连接 CE , DE . AC 与 DE 相交于点 F .
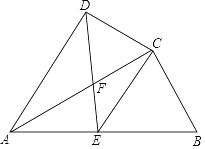
(1)求证: △ ADF ∽△ CEF ;
(2)若 AD=4 , AB=6 ,求 ![]() 的值.
的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由角平分线的定义证明 ∠ DAC= ∠ CAB ,根据直角三角形斜边上的中线等于斜边的一半及等边对等角,证明 ∠ DAC= ∠ ECA ,得到 CE ∥ AD ,进而得到 △ ADF ∽△ CEF ;
(2)由△ AFD ∽△ CFE ;根据相似三角形的性质得出 AD ∶CE=AF :CF ;进而得出答案.
(1)证明: ∵ AC 平分 ∠ DAB ,
∴∠ DAC= ∠ CAB ,
∵ E 为 AB 的中点,
∴ CE=![]() AB=AE ,
AB=AE ,
∴∠ EAC= ∠ ECA ;
∵∠ DAC= ∠ CAB ,
∴∠ DAC= ∠ ECA ,
∴CE∥AD
∴△ ADF ∽△ CEF ,
(2)∵△ AFD ∽△ CFE ,
∴ AD∶ CE=AF ∶CF ;
∵ CE=![]() AB=3 , AD=4 ,
AB=3 , AD=4 ,
∴ ![]()
∴ ![]()
∴![]() =
=![]()

【题目】为切实加强中小学生交通安全宣传教育,让学生真正知危险、会避险,郑州市某中学开展了“交通安全进校园”系列活动.为了解七、八年级学生对交通安全知识的掌握情况,对七、八年级学生进行了测试,现从两年级中各随机抽取20名学生的测试成绩(百分制)进行整理、描述和分析(成绩不低于90分为优秀).
测试成绩(百分制)如下:
七年级:52,78,82,86,77,83,92,87,72,81,93,98,81,69,87,86,80,81,82,94
八年级:87,77,90,79,93,83,88,84,82,94,86,88,57,68,89,59,81,90,88,95
分组整理,描述数据
分组 | 七年级 | 八年级 | ||
画“正”计数 | 频数 | 画“正”计数 | 频数 | |
| 一 | 1 |
| 2 |
| 一 | 1 | 一 | 1 |
|
|
| 2 | |
|
| 正正 | 10 | |
|
| 4 | 正 | 5 |
七、八年级抽取学生的测试成绩统计表
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 82 |
| 81 | 20% |
八年级 | 82.5 | 86.5 |
| 25% |
根据以上信息,回答下列问题:
(1)表中![]() __________,
__________,![]() __________,
__________,![]() __________,
__________,![]()
(2)若该校七年级270人和八年级280人参加了此次测试,估计参加此次测试成绩优秀的学生人数;
(3)根据以上数据,你认为该校七、八年级哪个年级学生掌握交通安全知识较好?并说明理由?