Question

【题目】已知抛物线经过两点．

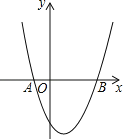
（1）求抛物线的解析式和顶点坐标；

（2）设点为抛物线上一点，若，求点的坐标．

Answer 1

【答案】（1）抛物线的解析式为，顶点坐标为 （2）点坐标为，

【解析】试题分析：（1）由点A、B的坐标利用待定系数法即可求出抛物线的解析式，再利用配方法即可求出抛物线顶点坐标；

（2）设P（x，y），根据三角形的面积公式以及S△PAB＝6，即可算出y的值，代入抛物线解析式即可得出点P的坐标．

试题解析：

解：（1）把A（－1，0）、B（3，0）分别代入y＝x2＋bx＋c中，

得： ，

解得： ，

∴抛物线的解析式为y＝x2－2x－3．

∵y＝ x2－2x－3＝(x－1)2－4，

∴顶点坐标为（1，－4）．

（2）∵A（－1，0）、B（3，0），∴AB＝4．

设P（x，y），则S△PAB＝AB|y|＝2|y|＝6，

∴|y|＝3，

∴y＝±3．

①当y＝3时，x2－2x－3＝3，解得：x1＝1＋，x2＝1－，

此时P点坐标为（1＋，3）或（1－，3）；

②当y＝－3时，x2－2x－3＝－3，解得：x1＝0，x2＝2，

此时P点坐标为（0，－3）或（2，－3）．

综上所述，P点坐标为（1＋，3）或（1－，3）或（0，－3）或（2，－3）．