题目内容
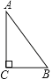
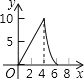
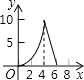
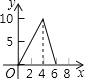
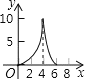
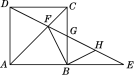
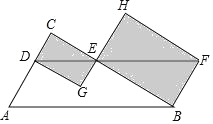
【题目】如图,在 △ ABC 中,∠ ACB=90° ,AC=BC=2 .E , F 分别是射线 AC 、CB 上的动点,且 AE=BF , EF 与 AB 交于点 G ,EH⊥ AB 于点 H ,设 AE=x ,GH=y ,下面能够反映 y 与 x 之间函数关系的图象是( )
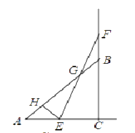
A.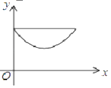 B.
B.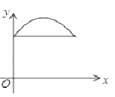 C.
C.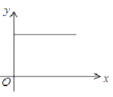 D.
D.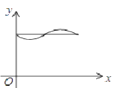
【答案】C
【解析】
先判断出 △ ABC 是等腰直角三角形,再判断出 △ AHE 是等腰直角三角形,然后根据勾股定理计算出 AB 、 AH 的长度,过点 B 作 BD ∥ AC 交 EF 于点 D ,然后利用平行线分线段成比例得出 B D:A E = B G:A G,B F:F C = B D:E C ,再表示出BD ,然后求出 BG 的长度,最后根据GH=AB﹣AH -BG ,代入数据就可以得出 y 关于 x 的函数关系式,再根据函数相应的图像解答.
解: ∵∠ ACB=90° , AC=BC=2 ,
∴△ABC是等腰直角三角形,
∴ AB=![]() , ∠ A=45° ,
, ∠ A=45° ,
∵ EH ⊥ AB 于点 H ,
∴△AHE是等腰直角三角形,
∵AC=BC=2
∴ AH=![]() AE=
AE=![]() x ,
x ,
过点 B作 BD∥AC交EF于点 D ,
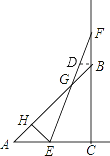
则
![]()
∴![]()
![]()
∴![]() =
=![]()
整理得, ![]()
解得, BG=![]() -
-![]() x ,
x ,
根据图形,GH=AB﹣AH﹣BG ,
=2![]() ﹣
﹣![]() x-(
x-(![]() -
-![]() x),
x),
=2![]() ﹣
﹣![]() x-
x-![]() +
+![]() x
x
=![]()
即 y=/span>![]() ,是一条平行于 x 轴的直线.
,是一条平行于 x 轴的直线.
故选: C ,

【题目】某公司生产的商品的市场指导价为每件150元,公司的实际销售价格可以浮动![]() 个百分点[即销售价格
个百分点[即销售价格![]() ],经过市场调研发现,这种商品的日销售量
],经过市场调研发现,这种商品的日销售量![]() (件)与销售价格浮动的百分点
(件)与销售价格浮动的百分点![]() 之间的函数关系如下:
之间的函数关系如下:
浮动 | 0 | 1 | 2 | 3 | … |
销售量 | 24 | 22 | 20 | 18 | … |
若该公司按浮动![]() 个百分点的价格出售,每件商品仍可获利10%.
个百分点的价格出售,每件商品仍可获利10%.
(1)求该公司生产每件商品的成本为多少元?
(2)当实际销售价格定为多少元时,日销售利润为660元?[说明:日销售利润![]() (销售价格
(销售价格![]() 成本)
成本)![]() 日销售量];
日销售量];
(3)该公司决定每销售一件商品就捐赠![]() 元利润(
元利润(![]() )给希望工程,公司通过销售记录发现,当价格浮动的百分点大于
)给希望工程,公司通过销售记录发现,当价格浮动的百分点大于![]() 时,扣除捐赠后的日销售利润随
时,扣除捐赠后的日销售利润随![]() 的增大而减小,直接写出
的增大而减小,直接写出![]() 的取值范围.
的取值范围.