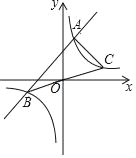
ΧβΡΩΡΎ»ί
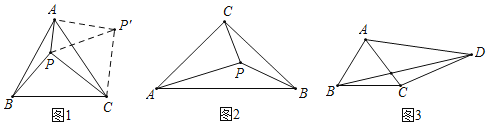
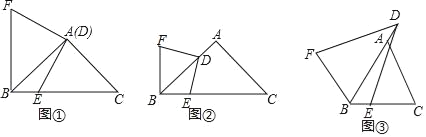
ΓΨΧβΡΩΓΩΙέ≤λ≤¬œκΘΚΘ®1Θ©»γΆΦΔΌΘ§‘ΎRtΓςABC÷–Θ§ΓœBACΘΫ90ΓψΘ§ABΘΫACΘΫ3Θ§ΒψD”κΒψA÷ΊΚœΘ§ΒψE‘Ύ±ΏBC…œΘ§Ν§Ϋ”DEΘ§ΫΪœΏΕΈDE»ΤΒψDΥ≥ ±’κ–ΐΉΣ90ΓψΒΟΒΫœΏΕΈDFΘ§Ν§Ϋ”BFΘ§BE”κBFΒΡΈΜ÷ΟΙΊœΒ «ΓΓ ΓΓΘ§BE+BFΘΫΓΓ ΓΓΘΜ
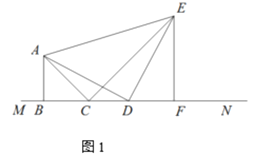
ΧΫΨΩ÷ΛΟςΘΚΘ®2Θ©‘ΎΘ®1Θ©÷–Θ§»γΙϊΫΪΒψD―ΊABΖΫœρ“ΤΕ·Θ§ ΙADΘΫ1Θ§Τδ”ύΧθΦΰ≤Μ±δΘ§»γΆΦΔΎΘ§≈–ΕœBE”κBFΒΡΈΜ÷ΟΙΊœΒΘ§≤Δ«σBE+BFΒΡ÷ΒΘ§«κ–¥≥ωΡψΒΡάμ”…ΜρΦΤΥψΙΐ≥ΧΘΜ
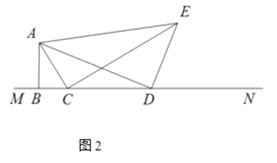
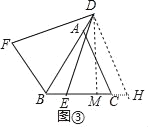
ΆΊ’Ι―”…λΘΚΘ®3Θ©»γΆΦΔέΘ§‘ΎΓςABC÷–Θ§ABΘΫACΘ§ΓœBACΘΫaΘ§ΒψD‘Ύ±ΏBAΒΡ―”≥ΛœΏ…œΘ§BDΘΫnΘ§Ν§Ϋ”DEΘ§ΫΪœΏΕΈDE»ΤΉ≈ΒψDΥ≥ ±’κ–ΐΉΣΘ§–ΐΉΣΫ«ΓœEDFΘΫaΘ§Ν§Ϋ”BFΘ§‘ρBE+BFΒΡ÷Β «Εύ…ΌΘΩ«κ”ΟΚ§”–nΘ§aΒΡ ΫΉ”÷±Ϋ”–¥≥ωΫα¬έΘ°
ΓΨ¥πΑΗΓΩΙέ≤λ≤¬œκΘΚΘ®1Θ©BFΓΆBEΘ§BCΘΜΧΫΨΩ÷ΛΟςΘΚΘ®2Θ©BFΓΆBEΘ§BF+BEΘΫ![]() Θ§ΦϊΫβΈωΘΜΆΊ’Ι―”…λΘΚΘ®3Θ©BF+BEΘΫ
Θ§ΦϊΫβΈωΘΜΆΊ’Ι―”…λΘΚΘ®3Θ©BF+BEΘΫ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©÷Μ“Σ÷ΛΟςΓςBAFΓ’ΓςCAEΘ§Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®2Θ©»γΆΦΔΎ÷–Θ§ΉςDHΓΈACΫΜBC”ΎHΘ°άϊ”ΟΘ®1Θ©÷–Ϋα¬έΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©»γΆΦΔέ÷–Θ§ΉςDHΓΈACΫΜBCΒΡ―”≥ΛœΏ”ΎHΘ§ΉςDMΓΆBC”ΎMΘ°÷Μ“Σ÷ΛΟςΓςBDFΓ’ΓςHDEΘ§Ω…÷ΛBF+BEΘΫBHΘ§Φ¥Ω…ΫβΨωΈ Χβ.
Θ®1Θ©»γΆΦΔΌ÷–Θ§
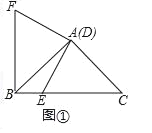
ΓΏΓœEAFΘΫΓœBACΘΫ90ΓψΘ§
ΓύΓœBAFΘΫΓœCAEΘ§
ΓΏAFΘΫAEΘ§ABΘΫACΘ§
ΓύΓςBAFΓ’ΓςCAEΘ§
ΓύΓœABFΘΫΓœCΘ§BFΘΫCEΘ§
ΓΏABΘΫACΘ§ΓœBACΘΫ90ΓψΘ§
ΓύΓœABCΘΫΓœCΘΫ45ΓψΘ§
ΓύΓœFBEΘΫΓœABF+ΓœABCΘΫ90ΓψΘ§BCΘΫBE+ECΘΫBE+BFΘ§
Ι ¥πΑΗΈΣBFΓΆBEΘ§BCΘΜ
Θ®2Θ©»γΆΦΔΎ÷–Θ§ΉςDHΓΈACΫΜBC”ΎHΘ§
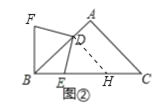
ÿDHøACȧ
ΓύΓœBDHΘΫΓœAΘΫ90ΓψΘ§ΓςDBH «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
”…Θ®1Θ©Ω…÷ΣΘ§BFΓΆBEΘ§BF+BEΘΫBHΘ§
ΓΏABΘΫACΘΫ3Θ§ADΘΫ1Θ§
ΓύBDΘΫDHΘΫ2Θ§
ΓύBHΘΫ2![]() Θ§
Θ§
ΓύBF+BEΘΫBHΘΫ2![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦΔέ÷–Θ§ΉςDHΓΈACΫΜBCΒΡ―”≥ΛœΏ”ΎHΘ§ΉςDMΓΆBC”ΎMΘ§
ÿACøDHȧ
ΓύΓœACHΘΫΓœHΘ§ΓœBDHΘΫΓœBACΘΫΠΝΘ§
ΓΏABΘΫACΘ§
ΓύΓœABCΘΫΓœACB
ΓύΓœDBHΘΫΓœHΘ§
ΓύDBΘΫDHΘ§
ΓΏΓœEDFΘΫΓœBDHΘΫΠΝΘ§
ΓύΓœBDFΘΫΓœHDEΘ§
ΓΏDFΘΫDEΘ§DBΘΫDHΘ§
ΓύΓςBDFΓ’ΓςHDEΘ§
ΓύBFΘΫEHΘ§
ΓύBF+BEΘΫEH+BEΘΫBHΘ§
ΓΏDBΘΫDHΘ§DMΓΆBHΘ§
ΓύBMΘΫMHΘ§ΓœBDMΘΫΓœHDMΘ§
ΓύBMΘΫMHΘΫBDsin![]() Θ°
Θ°
ΓύBF+BEΘΫBHΘΫ2nsin![]() Θ°
Θ°

 ΟœΫ®ΤΫ–Γ―ßΙωΕ·≤β ‘œΒΝ–¥πΑΗ
ΟœΫ®ΤΫ–Γ―ßΙωΕ·≤β ‘œΒΝ–¥πΑΗ