题目内容
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )
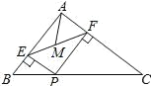
A.1B.1.3C.1.2D.1.5
【答案】C
【解析】
首先证明四边形AEPF为矩形,可得AM=![]() AP,最后利用垂线段最短确定AP的位置,利用面积相等求出AP的长,即可得AM.
AP,最后利用垂线段最短确定AP的位置,利用面积相等求出AP的长,即可得AM.
在△ABC中,因为AB2+AC2=BC2,
所以△ABC为直角三角形,∠A=90°,
又因为PE⊥AB,PF⊥AC,
故四边形AEPF为矩形,
因为M为EF中点,
所以M也是AP中点,即AM=![]() AP,
AP,
故当AP⊥BC时,AP有最小值,此时AM最小,
由![]() ,可得AP=
,可得AP=![]() ,
,
AM=![]() AP=
AP=![]()
故本题正确答案为C.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目