题目内容
【题目】如图,平面内的直线有相交和平行两种位置关系.
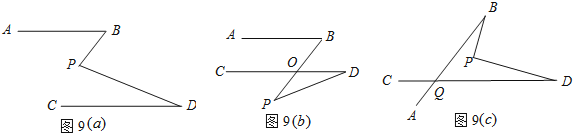
(1)如图(a),已知AB∥CD,求证:∠BPD=∠B+∠D.
(2)如图(b),已知AB∥CD,求证:∠BOD=∠P+∠D.
(3)根据图(c),试判断∠BPD,∠B,∠D,∠BQD之间的数量关系,并说明理由.
【答案】(1)见解析; (2) ∠BOD=∠P+∠D; (3) ∠BPD=∠B+∠BQD+∠D,理由见解析
【解析】
(1)过点P作PE∥AB,由平行线的性质“两直线平行,内错角相等”得出∠B=∠BPE、∠D=∠DPE,结合角之间的关系即可得出结论;
(2)过点P作PE∥CD,根据平行线的性质即可得出∠BOD=∠BPE、∠D=∠DPE,结合角之间的关系即可得出结论;
(3)数量关系:∠BPD=∠B+∠BQD+∠D.过点P作PE∥CD,过点B作BF∥PE,由平行线的性质得出“∠FBA+∠BQD=180°,∠FBP+∠BPE=180°,∠D=∠DPE”,再根据角之间的关系即可得出结论.
(1)证明:过点P作PE∥AB,如图1所示.

∵AB∥PE,AB∥CD,(已知)
∴AB∥PE∥CD.(在同一平面内,平行于同一直线的两条直线互相平行)
∴∠B=∠BPE,∠D=∠DPE,(两直线平行,内错角相等)
∴∠BPD=∠BPE+∠DPE=∠B+∠D.(等量代换)
(2)证明:过点P作PE∥CD,如图2所示.

∵PE∥CD,(辅助线)
∴∠BOD=∠BPE,(两直线平行,同位角相等);∠D=∠DPE,(两直线平行,内错角相等)
∴∠BPE=∠BPD+∠DPE=∠BPD+∠D,(等量代换)
即∠BOD=∠P+∠D.(等量代换)
(3)解:数量关系:∠BPD=∠B+∠BQD+∠D.
理由如下:
过点P作PE∥CD,过点B作BF∥PE,如图3所示.

则BF∥PE∥CD,
∴∠FBA+∠BQD=180°,∠FBP+∠BPE=180°,(两直线平行,同旁内角互补)
∠D=∠DPE,(两直线平行,内错角相等)
∵∠FBA=∠FBP+∠B,
∴∠BPE=∠BQD+∠B,
∴∠BPD=∠BPE+∠DPE=∠BQD+∠B+∠D.(等量代换)

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案