题目内容
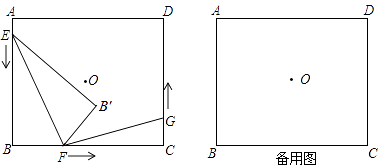
【题目】如图，在ABCD中，AB=6cm，AD=9cm，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=4 
cm，则EF+CF的长为cm． 
【答案】5
【解析】解：∵AE平分∠BAD， ∴∠DAE=∠BAE；
又∵AD∥BC，
∴∠BEA=∠DAE=∠BAE，
∴AB=BE=6cm，
∴EC=9﹣6=3（cm），
∵BG⊥AE，垂足为G，
∴AE=2AG．
在Rt△ABG中，∵∠AGB=90°，AB=6cm，BG=4 
cm，
∴AG= 
=2（cm），
∴AE=2AG=4cm；
∵EC∥AD，
∴ 
= 
= 
= 
= 
，
∴ 
= ， 
= ，
解得：EF=2（cm），FC=3（cm），
∴EF+CF的长为5cm．
所以答案是：5．
【考点精析】本题主要考查了勾股定理的概念和平行四边形的性质的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．
【题目】在不透明的袋子中有四张标着数字1，2，3，4的卡片，小明、小华两人按照各自的规则玩抽卡片游戏． 小明画出树状图如图所示：
小华列出表格如下：
第一次 | 1 | 2 | 3 | 4 |
1 | （1，1） | （2，1） | （3，1） | （4，1） |
2 | （1，2） | （2，2） | ① | （4，2） |
3 | （1，3） | （2，3） | （3，3） | （4，3） |
4 | （1，4） | （2，4） | （3，4） | （4，4） |
回答下列问题：
（1）根据小明画出的树形图分析，他的游戏规则是，随机抽出一张卡片后（填“放回”或“不放回”），再随机抽出一张卡片；
（2）根据小华的游戏规则，表格中①表示的有序数对为；
（3）规定两次抽到的数字之和为奇数的获胜，你认为谁获胜的可能性大？为什么？
