题目内容
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(2 ,AB=4
,AB=4 ,直线
,直线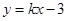 与x轴、y轴分别交于C 、D两点,∠OCD=60°
与x轴、y轴分别交于C 、D两点,∠OCD=60°
(1)设⊙P的半径为r,则r= (3分)
(2)求k的值. (4分)
(3)将⊙P沿直线x= 向下平移,当⊙P与直线CD相切于点E时,求点E的坐标. (6分)
向下平移,当⊙P与直线CD相切于点E时,求点E的坐标. (6分)
 ,AB=4
,AB=4 ,直线
,直线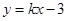 与x轴、y轴分别交于C 、D两点,∠OCD=60°
与x轴、y轴分别交于C 、D两点,∠OCD=60°
(1)设⊙P的半径为r,则r= (3分)
(2)求k的值. (4分)
(3)将⊙P沿直线x=
 向下平移,当⊙P与直线CD相切于点E时,求点E的坐标. (6分)
向下平移,当⊙P与直线CD相切于点E时,求点E的坐标. (6分)解:(1) r=3 ………………………3分
(2) ………………………7分
………………………7分
(3)∴E( ,
, )或(
)或( ,
, )
)
(2)
 ………………………7分
………………………7分(3)∴E(
 ,
, )或(
)或( ,
, )
) 本试题主要是考查了一次函数以及直线与圆的相切的知识的和运用。
(1)根据圆心距和半径以及半弦长之间勾股定理可知得到结论。
(2)∵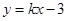
∴D(0,—3) OD=3∵∠OCD=60° ∴∠DCO=30° ∴CD=2CO,结合三角形三边的勾股定理得到OC= ,进而求解得到k的值。
,进而求解得到k的值。
(3)需要对于点圆P与直线相切于点的位置进行讨论,结合角度和长度得到切点的坐标,进而得到结论。
(1)根据圆心距和半径以及半弦长之间勾股定理可知得到结论。
(2)∵
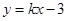
∴D(0,—3) OD=3∵∠OCD=60° ∴∠DCO=30° ∴CD=2CO,结合三角形三边的勾股定理得到OC=
 ,进而求解得到k的值。
,进而求解得到k的值。(3)需要对于点圆P与直线相切于点的位置进行讨论,结合角度和长度得到切点的坐标,进而得到结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
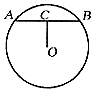
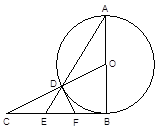
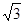 ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径; 
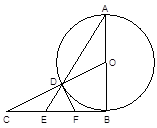
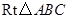 中,斜边AB=13cm,以直线BC为轴旋转一周,得到一个侧面积为65
中,斜边AB=13cm,以直线BC为轴旋转一周,得到一个侧面积为65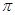
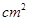 的圆锥,则BC="_______" cm.
的圆锥,则BC="_______" cm.