题目内容
武当山风景管理区，为提高游客到某景点的安全性，决定将到达该景点的步行台阶进行改善，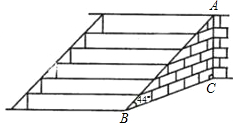
把倾角由44°减至32°，已知原台阶AB的长为5米（BC所在地面为水平面）．
（1）改善后的台阶会加长多少？（精确到0.01米）
（2）改善后的台阶多占多长一段地面？（精确到0.01米）
把倾角由44°减至32°，已知原台阶AB的长为5米（BC所在地面为水平面）．（1）改善后的台阶会加长多少？（精确到0.01米）
（2）改善后的台阶多占多长一段地面？（精确到0.01米）
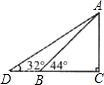
（1）如图，在Rt△ABC中，AC=AB•sin44°=5sin44°≈3.473（米）．
在Rt△ACD中，AD=
=
≈6.554（米），∴AD-AB=6.554-5≈1.55（米）．
答：改善后的台阶会加长1.55米．
（2）如图，在Rt△ABC中，BC=AB•cos44°=5cos44°≈3.597（米）．
在Rt△ACD中，CD=
=
≈5.558（米）．
∴BD=CD-BC=5.558-3.597≈1.96（米）．
答：改善后的台阶多占1.96米长的一段地面．
在Rt△ACD中，AD=
| AC |
| sin32° |
| 3.473 |
| sin32° |
答：改善后的台阶会加长1.55米．
（2）如图，在Rt△ABC中，BC=AB•cos44°=5cos44°≈3.597（米）．
在Rt△ACD中，CD=
| AC |
| tan32° |
| 3.473 |
| tan32° |
∴BD=CD-BC=5.558-3.597≈1.96（米）．
答：改善后的台阶多占1.96米长的一段地面．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
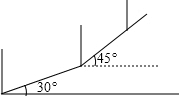
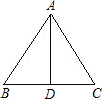
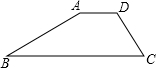（斜坡CD）的坡度为i=1：1，
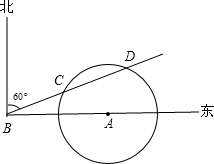北偏东60°的BD方向移动，在距离台风中心130km内的地方都要受到其影响．
